Prijava z e-naslovom
Prijava brez gesla
Trikotnik konstruiramo na podlagi poznavanja konstrukcije osnovnih geometrijskih elementov in kotov.
Za konstrukcijo trikotnika potrebujemo tri neodvisne podatke. Ti podatki so kombinacija:
stranic
notranjih kotov
višin
težiščnic
Pred vsako konstrukcijo trikotnika narišemo skico, ki nam služi za orientacijo pri risanju. Na skici po možnosti označimo vsak podatek s svojo barvo.
V nadaljevanju so opisani koraki konstrukcije za različne kombinacije podatkov. Navedeni so tudi pogoji za izvedbo konstrukcije, če ti obstajajo.
Posamična konstrukcija ima lahko več možnih rešitev. Spodnja predpostavka število rešitev nekoliko omeji in s tem ohranja preglednost gradiva:
Konstrukcije z več možnimi rešitvami so izvedene ob predpostavki, da je trikotnik pozitivno usmerjen ter ima vse kote ostre.
Nekatere konstrukcije imajo kljub zgornji predpostavki še vedno dve rešitvi. V takem primeru sta prikazani obe.
Če imamo podane tri stranice, lahko začnemo risati katero koli stranico in potem dodamo ostali dve.
Pogoj za izvedbo konstrukcije
Konstrukcija je možna ob zadoščenem pogoju trikotniške neenakosti:
Vsota dolžin katerihkoli dveh stranic trikotnika je večja od dolžine tretje stranice:
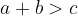
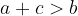
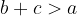
V nadaljevanju so našteti koraki za primer, ko konstrukcijo začnemo pri stranici c.
Skica
1. korak
Narišemo daljico dolžine c. Končni točki daljice označimo z A in B:
Daljica AB predstavlja stranico c trikotnika, A in B pa sta dve izmed treh oglišč trikotnika.
2. korak
V šestilo vzamemo dolžino stranice b.
Šestilo zapičimo v točko A.
S šestilom zarišemo krožni lok v smeri proti oglišču C trikotnika (glej skico):
3. korak
V šestilo vzamemo dolžino stranice a.
Šestilo zapičimo v točko B.
S šestilom zarišemo krožni lok v smeri proti oglišču C trikotnika (glej skico), tako da seka predhodno narisan krožni lok. Presečišče krožnih lokov označimo s točko C:
4. korak
Z ravnilom povežemo točki A in C:
Daljica AC predstavlja stranico b trikotnika.
5. korak
Z ravnilom povežemo še točki B in C:
Daljica BC predstavlja stranico a trikotnika.
Možni so trije načini podajanja stranic in vmesnega kota:
V nadaljevanju so opisani koraki za prvo kombinacijo iz zgornje tabele.
Pogoj za izvedbo konstrukcije
Konstrukcija je možna, če je podani kot večji od 0° in manjši od 180°.
Pogoj za prvo kombinacijo iz tabele se glasi:
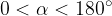
Pogoj izvira iz izreka o vsoti notranjih kotov v trikotniku:
Vsota notranjih kotov trikotnika je 180°.
Skica
1. korak
Narišemo daljico dolžine c. Končni točki daljice označimo z A in B:
Daljica AB predstavlja stranico c trikotnika, A in B pa sta dve izmed treh oglišč trikotnika.
2. korak
Konstruiramo kot 
z vrhom v točki A. En krak kota sovpada z nosilko daljice AB, drugi krak pa je usmerjen proti oglišču C trikotnika (glej skico):
3. korak
V šestilo vzamemo dolžino stranice b.
Šestilo zapičimo v točko A.
S šestilom zarišemo krožni lok v smeri proti oglišču C trikotnika (glej skico), tako da seka krak kota . Tako nastalo presečišče označimo s točko C:
Daljica AC predstavlja stranico b trikotnika, točka C pa je tretje oglišče trikotnika.
4. korak
Z ravnilom povežemo še točki B in C:
Daljica BC predstavlja stranico a trikotnika.
Možni so trije načini podajanja stranice in kotov ob tej stranici:
V nadaljevanju so opisani koraki za prvo kombinacijo iz zgornje tabele.
Pogoj za izvedbo konstrukcije
Konstrukcija je možna, če je vsota podanih kotov večja od 0° in manjša od 180°.
Pogoj za prvo kombinacijo iz tabele se glasi:
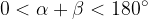
Pogoj izvira iz izreka o vsoti notranjih kotov v trikotniku:
Vsota notranjih kotov trikotnika je 180°.
Skica
1. korak
Narišemo daljico dolžine c. Končni točki daljice označimo z A in B:
Daljica AB predstavlja stranico c trikotnika, A in B pa sta dve izmed treh oglišč trikotnika.
2. korak
Konstruiramo kot z vrhom v točki A. En krak kota sovpada z nosilko daljice AB, drugi krak pa je usmerjen proti oglišču C trikotnika (glej skico):
3. korak
Konstruiramo kot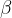 
z vrhom v točki B. En krak kota sovpada z nosilko daljice AB, drugi krak pa je usmerjen proti oglišču C trikotnika (glej skico). Točko, kjer se sekata poševna kraka kotov in 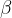označimo s C:
Daljica AC predstavlja stranico b, daljica BC stranico a, točka C pa je tretje oglišče trikotnika:
Možnih je šest načinov tovrstnega podajanja stranic in kota:
V nadaljevanju so opisani koraki za prvo kombinacijo iz zgornje tabele.
Pogoj za izvedbo konstrukcije
Konstrukcija je možna, če je podani kot večji od 0° in manjši od 180°.
Pogoj za prvo kombinacijo iz tabele se glasi:
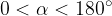
Pogoj izvira iz izreka o vsoti notranjih kotov v trikotniku:
Vsota notranjih kotov trikotnika je 180°.
Skica
1. korak
Narišemo daljico dolžine a. Končni točki daljice označimo z B in C (glej skico):
Daljica BC predstavlja stranico a trikotnika, B in C pa sta dve izmed treh oglišč trikotnika.
2. korak
Konstruiramo kot 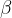z vrhom v točki B. En krak kota sovpada z nosilko daljice BC, drugi krak pa je usmerjen proti oglišču A trikotnika (glej skico):
3. korak
V šestilo vzamemo dolžino stranice b.
Šestilo zapičimo v točko C.
S šestilom zarišemo krožni lok v smeri proti oglišču A trikotnika (glej skico), tako da seka vodoravni krak kota 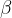. Tako nastalo presečišče označimo s točko A:
Daljica AB predstavlja stranico c trikotnika, točka A pa je tretje oglišče trikotnika:
4. korak
Z ravnilom povežemo še točki A in C:
Daljica AC predstavlja stranico b trikotnika.
Možnih je šest načinov tovrstnega podajanja stranic in višine:
V nadaljevanju so opisani koraki za prvo kombinacijo iz zgornje tabele.
Pogoj za izvedbo konstrukcije
Konstrukcija je možna, če je podana višina krajša od tiste podane stranice, ki ne pripada tej višini.
Pogoj za prvo kombinacijo iz tabele se glasi:
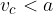
Pogoj izvira iz Pitagorovega izreka; v pravokotnem trikotniku je katera koli kateta vedno krajša od hipotenuze.
Ob omenjenem pogoju ima naloga dve možni rešitvi.
Dopuščamo tudi možnost, da sta obravnavani višina in stranica enako dolgi; v tem primeru je rešitev naloge le ena.
Skica
1. korak
Narišemo daljico dolžine c. Končni točki daljice označimo z A in B (glej skico):
Daljica AB predstavlja stranico c trikotnika, A in B pa sta dve izmed treh oglišč trikotnika.
2. korak
Narišemo vzporednico daljici AB na razdalji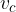 
in jo označimo s p:
3. korak
V šestilo vzamemo dolžino stranice a.
Šestilo zapičimo v točko B.
S šestilom zarišemo krožni lok v smeri proti premici p.
Dobimo dve presečišči krožnega loka in premice. Označimo ju s točkama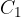 
in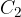 
:
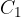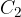Točki in predstavljata dve možni lokaciji za tretje oglišče trikotnika.
V nadaljevanju sta prikazani konstrukciji za obe možnosti položaja oglišča C:
4. korak
(a) Rešitev 1:
Z ravnilom povežemo točki B in .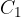
Daljica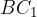 
predstavlja stranico a trikotnika. Ker predstavlja prvo možno rešitev, ima dodan indeks 1. Na spodnji sliki je označena pikčasto.
(b) Rešitev 2:
Z ravnilom povežemo točki B in .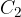
Daljica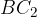 
predstavlja stranico a trikotnika. Ker predstavlja drugo možno rešitev, ima dodan indeks 2. Na spodnji sliki je označena črtkano:
5. korak
(a) Rešitev 1:
Z ravnilom povežemo točki A in .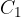
Daljica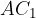 
predstavlja stranico b trikotnika. Ker predstavlja prvo možno rešitev, ima dodan indeks 1. Na spodnji sliki je označena pikčasto.
(b) Rešitev 2:
Z ravnilom povežemo točki A in .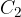
Daljica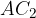 
predstavlja stranico b trikotnika. Ker predstavlja drugo možno rešitev, ima dodan indeks 2. Na spodnji sliki je označena črtkano:
Možni so trije načini tovrstnega podajanja stranic in višine:
V nadaljevanju so opisani koraki za prvo kombinacijo iz zgornje tabele.
Pogoj za izvedbo konstrukcije
Konstrukcija je možna, če sta obe podani stranici daljši od podane višine.
Pogoj za prvo kombinacijo iz tabele se glasi:
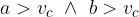
Pogoj izvira iz Pitagorovega izreka; v pravokotnem trikotniku je katera koli kateta vedno krajša od hipotenuze.
Skica
1. korak
Narišemo daljico dolžine 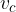. Končni točki daljice označimo s C in D (glej skico):
Daljica CD predstavlja višino na stranico c trikotnika, C pa je eno izmed treh oglišč trikotnika.
2. korak
V točki D narišemo pravokotnico na daljico CD in jo označimo s p:
3. korak
V šestilo vzamemo dolžino stranice b.
Šestilo zapičimo v točko C.
S šestilom zarišemo krožni lok v smeri proti oglišču A trikotnika (glej skico), tako da seka premico p. Tako nastalo presečišče označimo s točko A:
4. korak
Z ravnilom povežemo točki A in C:
Daljica AC predstavlja stranico b trikotnika.
5. korak
V šestilo vzamemo dolžino stranice a.
Šestilo zapičimo v točko C.
S šestilom zarišemo krožni lok v smeri proti oglišču B trikotnika (glej skico), tako da seka premico p. Tako nastalo presečišče označimo s točko B:
6. korak
Z ravnilom povežemo še točki B in C ter točki A in B:
Daljica BC predstavlja stranico a, daljica AB pa stranico c trikotnika.
Možni so trije načini tovrstnega podajanja kotov in višine:
V nadaljevanju so opisani koraki za prvo kombinacijo iz zgornje tabele.
Pogoj za izvedbo konstrukcije
Konstrukcija je možna, če je podana stranica daljša od tiste podane višine, ki ne pripada tej stranici.
Pogoj za prvo kombinacijo iz tabele se glasi:
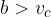
Pogoj izvira iz Pitagorovega izreka; v pravokotnem trikotniku je katera koli kateta vedno krajša od hipotenuze.
Skica
1. korak
Narišemo vzporednici z medsebojno razdaljo 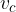ter jih označimo s p in q:
2. korak
Na premici q označimo poljubno točko A:
Točka A predstavlja eno izmed treh oglišč trikotnika.
3. korak
V šestilo vzamemo dolžino stranice b.
Šestilo zapičimo v točko A.
S šestilom zarišemo krožni lok v smeri proti oglišču C trikotnika (glej skico), tako da seka premico p. Tako nastalo presečišče označimo s točko C:
Točka C predstavlja drugo oglišče trikotnika.
4. korak
Z ravnilom povežemo točki A in C:
Daljica AC predstavlja stranico b trikotnika.
5. korak
Narišemo vzporednico daljici AC na razdalji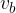 
in jo označimo z r.
Točko, kjer premica r seka premico q, označimo z B:
Daljica AB predstavlja stranico c trikotnika, točka B pa je tretje oglišče trikotnika.
6. korak
Z ravnilom povežemo točki B in C:
Daljica BC predstavlja stranico a trikotnika.
Možni so trije načini tovrstnega podajanja kotov in višine:
V nadaljevanju so opisani koraki za prvo kombinacijo iz zgornje tabele.
Pogoj za izvedbo konstrukcije
Konstrukcija je možna, če je vsota podanih kotov večja od 0° in manjša od 180°.
Pogoj za prvo kombinacijo iz tabele se glasi:
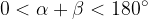
Pogoj izvira iz izreka o vsoti notranjih kotov v trikotniku:
Vsota notranjih kotov trikotnika je 180°.
Skica
1. korak
Konstruiramo kot z vrhom v točki A. Točka A predstavlja prvo oglišče trikotnika. Vodoravni krak kota je usmerjen proti oglišču B, poševni krak pa proti oglišču C trikotnika (glej skico):
2. korak
Narišemo vzporednico vodoravnemu kraku kota na razdalji 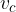in jo označimo s p
Točko, kjer premica p seka poševni krak kota , označimo s C:
Točka C predstavlja drugo oglišče, daljica AC pa stranico b trikotnika.
3. korak
Na vodoravnemu kraku kota označimo poljubno točko D.
Konstruiramo kot 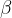z vrhom v točki D tako, da vodoravna kraka kotov in 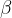sovpadata in sta nasprotno usmerjena.
4. korak
Narišemo vzporednico poševnemu kraku kota 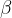skozi točko C in jo označimo s q
Točko, kjer premica q seka vodoravni krak kota oz. 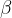, označimo z B
Točka B predstavlja tretje oglišče trikotnika, daljica BC stranico a, daljica AB pa stranico c trikotnika.
Možni so trije načini tovrstnega podajanja kotov in višine:
V nadaljevanju so opisani koraki za prvo kombinacijo iz zgornje tabele.
Pogoj za izvedbo konstrukcije
Konstrukcija je možna, če je vsota podanih kotov večja od 0° in manjša od 180°.
Pogoj za prvo kombinacijo iz tabele se glasi:
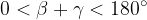
Pogoj izvira iz izreka o vsoti notranjih kotov v trikotniku:
Vsota notranjih kotov trikotnika je 180°.
Skica
1. korak
Narišemo vzporednici z medsebojno razdaljo 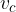ter jih označimo s p in q:
2. korak
Na premici q označimo poljubno točko B.
Konstruiramo kot 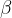z vrhom v točki B. En krak kota sovpada s premico q, drugi krak pa je usmerjen proti premici p.
Točko, kjer krak kota 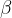seka premico p, označimo s C:
Daljica BC predstavlja stranico a trikotnika, B in C pa sta dve izmed treh oglišč trikotnika.
3. korak
Konstruiramo kot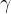 
z vrhom v točki C. En krak kota sovpada z daljico BC, drugi krak pa je usmerjen proti točki A (glej skico).
Točko, kjer krak kota 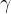seka premico q, označimo z A:
Točka A predstavlja tretje oglišče trikotnika, daljica AB stranico c, daljica AC pa stranico a trikotnika:
Možni so trije načini tovrstnega podajanja kotov in višine:
V nadaljevanju so opisani koraki za prvo kombinacijo iz zgornje tabele.
Pogoj za izvedbo konstrukcije
Konstrukcija je možna, če je podani kot večji od 0° in manjši od 180°.
Pogoj za prvo kombinacijo iz tabele se glasi:
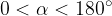
Pogoj izvira iz izreka o vsoti notranjih kotov v trikotniku:
Vsota notranjih kotov trikotnika je 180°.
Skica
1. korak
Konstruiramo kot z vrhom v točki A. Točka A predstavlja prvo oglišče trikotnika. Vodoravni krak kota je usmerjen proti oglišču B, poševni krak pa proti oglišču C trikotnika (glej skico):
2. korak
Narišemo vzporednico vodoravnemu kraku kota na razdalji 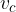in jo označimo s p
Točko, kjer premica p seka poševni krak kota , označimo s C:
Točka C predstavlja drugo oglišče, daljica AC pa stranico b trikotnika.
3. korak
Narišemo vzporednico poševnemu kraku kota na razdalji 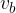in jo označimo z r
Točko, kjer premica r seka vodoravni krak kota , označimo z B:
Točka B predstavlja tretje oglišče trikotnika.
4. korak
Z ravnilom povežemo točki B in C ter točki A in B:
Daljica BC predstavlja stranico a, daljica AB pa stranico c trikotnika.
Možnih je šest načinov tovrstnega podajanja stranice, kota in višine:
V nadaljevanju so opisani koraki za prvo kombinacijo iz zgornje tabele.
Pogoj za izvedbo konstrukcije
Konstrukcija je možna, če je:
podana višina krajša od podane stranice.
Prvi pogoj za prvo kombinacijo iz tabele se glasi:
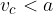
Pogoj izvira iz Pitagorovega izreka; v pravokotnem trikotniku je katera koli kateta vedno krajša od hipotenuze.
podani kot večji od 0° in manjši od 180°.
Drugi pogoj za prvo kombinacijo iz tabele se glasi:
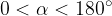
Pogoj izvira iz izreka o vsoti notranjih kotov v trikotniku:
Vsota notranjih kotov trikotnika je 180°.
Skica
1. korak
Konstruiramo kot z vrhom v točki A. Točka A predstavlja prvo oglišče trikotnika. Vodoravni krak kota je usmerjen proti oglišču B, poševni krak pa proti oglišču B trikotnika (glej skico):
2. korak
Narišemo vzporednico vodoravnemu kraku kota na razdalji 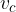in jo označimo s p
Točko, kjer premica p seka poševni krak kota , označimo s C:
Daljica AC predstavlja stranico b trikotnika, točka C pa je drugo oglišče trikotnika.
3. korak
V šestilo vzamemo dolžino stranice a.
Šestilo zapičimo v točko C.
S šestilom zarišemo krožni lok v smeri proti oglišču B trikotnika (glej skico), tako da seka vodoravni krak kota . Tako nastalo presečišče označimo s točko B:
Točka B predstavlja tretje oglišče trikotnika.
4. korak
Z ravnilom povežemo točki B in C ter točki A in B:
Daljica BC predstavlja stranico a, daljica AB pa stranico c trikotnika.
Možnih je šest načinov tovrstnega podajanja stranice, kota in višine:
V nadaljevanju so opisani koraki za prvo kombinacijo iz zgornje tabele.
Pogoj za izvedbo konstrukcije
Konstrukcija je možna, če je podani kot večji od 0° in manjši od 180°.
Pogoj za prvo kombinacijo iz tabele se glasi:
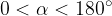
Pogoj izvira iz izreka o vsoti notranjih kotov v trikotniku:
Vsota notranjih kotov trikotnika je 180°.
Skica
1. korak
Narišemo daljico dolžine c. Končni točki daljice označimo z A in B (glej skico):
Daljica AB predstavlja stranico c trikotnika, A in B pa sta dve izmed treh oglišč trikotnika.
2. korak
Konstruiramo kot z vrhom v točki A. En krak kota sovpada z nosilko daljice AB, drugi krak pa je usmerjen proti oglišču C trikotnika (glej skico):
3. korak
Narišemo vzporednico daljici AB na razdalji 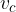in jo označimo s p
Točko, kjer premica p seka krak kota , označimo s C:
Točka C predstavlja tretje oglišče, daljica AC pa predstavlja stranico b trikotnika:
4. korak
Z ravnilom povežemo točki B in C:
Daljica BC predstavlja stranico a trikotnika.
Možnih je šest načinov tovrstnega podajanja stranic in težiščnice:
V nadaljevanju so opisani koraki za prvo kombinacijo iz zgornje tabele.
Pogoj za izvedbo konstrukcije
Konstrukcija je možna ob zadoščenem pogoju trikotniške neenakosti v manjšem trikotniku, ki ga sestavljajo polovica prve podane stranice in težiščnica nanjo ter druga stranica.
Za prvo kombinacijo to pomeni:
Vsota dolžin katerihkoli dveh stranic v manjšem trikotniku je večja od dolžine tretje stranice le-tega:
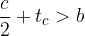
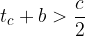
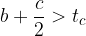
Skica
1. korak
Narišemo daljico dolžine c. Končni točki daljice označimo z A in B (glej skico):
Daljica AB predstavlja stranico c trikotnika, A in B pa sta dve izmed treh oglišč trikotnika.
2. korak
Konstruiramo razpolovišče daljice AB in ga označimo s točko D:
3. korak
V šestilo vzamemo dolžino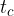 
.
Šestilo zapičimo v točko D.
S šestilom zarišemo krožni lok v smeri proti oglišču C trikotnika (glej skico):
4. korak
V šestilo vzamemo dolžino stranice b.
Šestilo zapičimo v točko A.
S šestilom zarišemo krožni lok v smeri proti oglišču C trikotnika (glej skico), tako da seka predhodno narisan krožni lok. Presečišče krožnih lokov označimo s točko C:
Točka C predstavlja tretje oglišče trikotnika.
5. korak
Z ravnilom povežemo točki A in C:
Daljica AC predstavlja stranico b, daljica DC pa težiščnico na stranico c trikotnika.
6. korak
Z ravnilom povežemo še točki B in C:
Daljica BC predstavlja stranico a trikotnika.
Možnih je šest načinov tovrstnega podajanja kota, stranice in težiščnice:
V nadaljevanju so opisani koraki za prvo kombinacijo iz zgornje tabele.
Pogoj za izvedbo konstrukcije
Konstrukcija je možna, če je podani kot večji od 0° in manjši od 180°.
Pogoj za prvo kombinacijo iz tabele se glasi:
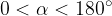
Pogoj izvira iz izreka o vsoti notranjih kotov v trikotniku:
Vsota notranjih kotov trikotnika je 180°.
Skica
1. korak
Konstruiramo kot z vrhom v točki A. Točka A predstavlja prvo oglišče trikotnika. Vodoravni krak kota je usmerjen proti oglišču B, poševni krak pa proti oglišču C trikotnika (glej skico):
2. korak
V šestilo vzamemo dolžino stranice b.
Šestilo zapičimo v točko A.
S šestilom zarišemo krožni lok v smeri proti oglišču C trikotnika (glej skico), tako da seka krak kota . Tako nastalo presečišče označimo s točko C:
Daljica AC predstavlja stranico b trikotnika, točka C pa je drugo oglišče trikotnika.
3. korak
Konstruiramo razpolovišče daljice AC in ga označimo s točko D:
4. korak
V šestilo vzamemo dolžino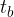 
.
Šestilo zapičimo v točko D.
S šestilom zarišemo krožni lok tako, tako da seka vodoravni krak kota . Tako nastalo presečišče označimo s točko B:
Točka B predstavlja tretje oglišče trikotnika.
5. korak
Z ravnilom povežemo točki B in C.
Daljica BC predstavlja stranico a, daljica DB pa težiščnico na stranico b trikotnika:
Daljica AB predstavlja stranico c trikotnika:
Možni so trije načini tovrstnega podajanja stranice, višine in težiščnice:
V nadaljevanju so opisani koraki za prvo kombinacijo iz zgornje tabele.
Pogoj za izvedbo konstrukcije
Konstrukcija je možna, če je podana višina krajša od podane težiščnice.
Pogoj za prvo kombinacijo iz tabele se glasi:
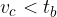
Pogoj izvira iz Pitagorovega izreka; v pravokotnem trikotniku je katera koli kateta vedno krajša od hipotenuze.
Ob omenjenem pogoju ima naloga dve možni rešitvi.
Dopuščamo tudi možnost, da sta podani višina in težiščnica enako dolgi; v tem primeru je rešitev naloge le ena.
Skica
1. korak
Narišemo daljico dolžine c. Končni točki daljice označimo z A in B (glej skico):
Daljica AB predstavlja stranico c trikotnika, A in B pa sta dve izmed treh oglišč trikotnika.
2. korak
Narišemo vzporednico daljici AB na razdalji 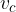in jo označimo s p:
3. korak
Konstruiramo razpolovišče daljice AB in ga označimo s točko D:
4. korak
V šestilo vzamemo dolžino .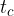
Šestilo zapičimo v točko D.
S šestilom zarišemo krožni lok v smeri proti premici p:
Dobimo dve presečišči krožnega loka in premice. Označimo ju s točkama 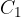in :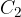
Točka C predstavlja tretje oglišče trikotnika. Ker ima konstrukcija dve možni rešitvi, točko označimo 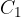s oz. s .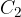
5. korak
(a) Rešitev 1:
Z ravnilom povežemo točki B in .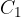
Daljica 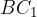predstavlja stranico a trikotnika. Ker predstavlja prvo možno rešitev, ima dodan indeks 1. Na spodnji sliki je označena pikčasto.
(b) Rešitev 2:
Z ravnilom povežemo točki B in .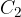
Daljica 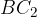predstavlja stranico a trikotnika. Ker predstavlja drugo možno rešitev, ima dodan indeks 2. Na spodnji sliki je označena črtkano:
Daljici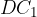 
in 
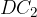predstavljata težiščnico na stranico c trikotnika. Težiščnici na stranico c sta v obeh rešitvah skladni.
6. korak
(a) Rešitev 1:
Z ravnilom povežemo točki A in .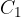
Daljica 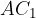predstavlja stranico b trikotnika. Ker predstavlja prvo možno rešitev, ima dodan indeks 1. Na spodnji sliki je označena pikčasto.
(b) Rešitev 2:
Z ravnilom povežemo točki A in .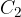
Daljica 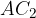predstavlja stranico b trikotnika. Ker predstavlja drugo možno rešitev, ima dodan indeks 2. Na spodnji sliki je označena črtkano:
Možnih je šest načinov tovrstnega podajanja kota, višine in težiščnice:
V nadaljevanju so opisani koraki za prvo kombinacijo iz zgornje tabele.
Pogoj za izvedbo konstrukcije
Konstrukcija je možna, če je podani kot večji od 0° in manjši od 180°.
Pogoj za prvo kombinacijo iz tabele se glasi:
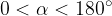
Pogoj izvira iz izreka o vsoti notranjih kotov v trikotniku:
Vsota notranjih kotov trikotnika je 180°.
Skica
1. korak
Konstruiramo kot z vrhom v točki A. Točka A predstavlja prvo oglišče trikotnika. Vodoravni krak kota je usmerjen proti oglišču B, poševni krak pa proti oglišču C trikotnika (glej skico):
2. korak
Narišemo vzporednico vodoravnemu kraku kota na razdalji 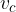in jo označimo s p
Točko, kjer premica p seka poševni krak kota , označimo s C:
Točka C predstavlja drugo oglišče, daljica AC pa stranico b trikotnika.
3. korak
Konstruiramo razpolovišče daljice AC in ga označimo s točko D:
4. korak
V šestilo vzamemo dolžino .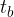
Šestilo zapičimo v točko D.
S šestilom zarišemo krožni lok v smeri proti oglišču B trikotnika (glej skico), tako da seka vodoravni krak kota . Tako nastalo presečišče označimo s točko B:
Točka B predstavlja tretje oglišče, daljica AB stranico c, daljica DB pa težiščnico na stranico b trikotnika:
5. korak
Z ravnilom povežemo točki B in C:
Daljica BC predstavlja stranico a trikotnika.
