Prijava z e-naslovom
Prijava brez gesla
V tem poglavju so predstavljeni koraki za konstruiranje posamičnih sestavnih delov trikotnika, s pomočjo katerih bomo v nadaljevanju konstruirali celoten trikotnik.
Stranico trikotnika konstruiramo na podlagi poznavanja konstrukcije daljice.
Vse stranice v trikotniku so daljice, njihova krajišča pa so oglišča trikotnika.
Ponovimo potek konstrukcije daljice AB, ki smo jo spoznali že v poglavju o konstruiranju osnovnih geometrijskih elementov:
Narišemo premico p, ki predstavlja nosilko daljice AB.
Na premici p označimo poljubno točko A.
V šestilo vzamemo dolžino daljice AB oz. stranice c.
Šestilo zapičimo v točko A.
S šestilom zarišemo krožni lok tako, da seka premico p:
Točko, v kateri krožni lok seka premico p, označimo z B:
Daljica AB predstavlja stranico c trikotnika. Analogno konstruiramo tudi ostale stranice v trikotniku.
Notranji kot v trikotniku konstruiramo na podlagi poznavanja konstrukcije ravninskega kota.
Vsak notranji kot v trikotniku je ravninski kot z vrhom v oglišču trikotnika, njegova kraka pa sta nosilki stranic, ki ta kot oklepata.
Spodnja skica prikazuje notranji kot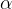 
, konstruiran po pravilih, podanih v poglavju Konstruiranje ravninskih kotov:
Analogno konstruiramo tudi ostale kote v trikotniku.
Višino trikotnika konstruiramo na podlagi poznavanja konstrukcije pravokotnice skozi točko izven premice.
Preden se lotimo risanja, ponovimo definicijo višine:
Višina trikotnika je daljica, ki povezuje oglišče trikotnika s pravokotno projekcijo tega oglišča na nosilko nasprotne stranice.
V trikotniku lahko konstruiramo tri višine:
višina na stranico a oziroma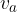 
višina na stranico b oziroma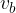 
višina na stranico c oziroma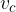 
V nadaljevanju so opisani koraki za konstrukcijo višine na stranico c:
1. korak
Narišemo nosilko daljice AB in jo označimo s p:
2. korak
Narišemo pravokotnico na premico p skozi točko C in jo označimo s q.
Presečišče premic p in q označimo s točko D:
Daljica CD predstavlja višino trikotnika na stranico c:
Na enak način konstruiramo tudi višine na ostali dve stranici.
Definicija višinske točke se glasi:
Višinska točka predstavlja presečišče vseh višin v trikotniku.
Za določitev višinske točke moramo torej konstruirati vsaj dve višini, tretja pa nam lahko služi za kontrolo:
Težiščnico trikotnika konstruiramo na podlagi poznavanja konstrukcije daljice in razpolovišča daljice.
Preden se lotimo risanja, ponovimo definicijo težiščnice:
Težiščnica trikotnika je daljica, ki povezuje oglišče trikotnika z razpoloviščem nasprotne stranice.
V trikotniku lahko konstruiramo tri težiščnice:
težiščnica na stranico a oziroma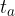 
težiščnica na stranico b oziroma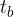 
težiščnica na stranico c oziroma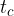 
V nadaljevanju so opisani koraki za konstrukcijo težiščnice na stranico c:
1. korak
Konstruiramo razpolovišče daljice AB in ga označimo s točko D:
2. korak
Z ravnilom povežemo točki C in D:
Daljica CD predstavlja težiščnico trikotnika na stranico c.
Na enak način konstruiramo tudi težiščnici na ostali dve stranici.
Definicija težišča se glasi:
Težišče predstavlja presečišče vseh težiščnic v trikotniku.
Za določitev težišča moramo torej konstruirati vsaj dve težiščnici, tretja pa nam lahko služi za kontrolo:
Trikotniku včrtamo krožnico na podlagi poznavanja konstrukcije simetrale kota in krožnice.
Preden se lotimo risanja, ponovimo definicijo:
Trikotniku včrtana krožnica ima središče v sečišču simetral notranjih kotov in se dotika vseh treh stranic trikotnika.
Konstrukcija trikotniku včrtane krožnice poteka po naslednjih korakih:
1. korak
Konstruiramo simetralo kota 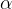in jo označimo z 
:
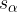2. korak
Konstruiramo simetralo kota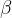 
in jo označimo z 
.
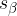Presečišče simetral 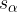in 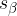označimo s točko S:
Točka S predstavlja središče trikotniku včrtane krožnice.
3. korak (poljubno)
Za kontrolo lahko konstruiramo še simetralo kota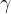 
in jo označimo z 
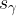. Če premica 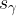poteka skozi točko S, smo bili pri risanju dovolj natančni:
4. korak
Poljubni stranici v trikotniku narišemo premico nosilko (npr. stranici c) in jo označimo s p:
5. korak
V šestilo vzamemo razdaljo med točko S in premico p.
Šestilo zapičimo v točko S.
S šestilom zarišemo krožnico:
Narisana krožnica je trikotniku včrtana krožnica.
Trikotniku očrtamo krožnico na podlagi poznavanja konstrukcije simetrale daljice in krožnice.
Preden se lotimo risanja, ponovimo definicijo:
Trikotniku očrtana krožnica ima središče v sečišču simetral stranic in poteka skozi vsa tri oglišča trikotnika.
Konstrukcija trikotniku očrtane krožnice poteka po naslednjih korakih:
1. korak
Konstruiramo simetralo stranice a in jo označimo z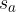 
:
2. korak
Konstruiramo simetralo stranice b in jo označimo z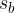 
:
Presečišče simetral 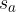in 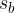označimo s točko S:
Točka S predstavlja središče trikotniku očrtane krožnice.
3. korak (poljubno)
Za kontrolo lahko konstruiramo še simetralo stranice c in jo označimo z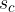 
. Če simetrala 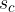: poteka skozi točko S, smo bili pri risanju dovolj natančni:
4. korak
V šestilo vzamemo razdaljo med točko S in poljubnim ogliščem trikotnika (npr. ogliščem A).
Šestilo zapičimo v točko S.
S šestilom zarišemo krožnico:
Narisana krožnica je trikotniku očrtana krožnica.
