Osebne zbirke


Nihanje je periodično (ponavljajoče) gibanje telesa okrog stabilne ravnovesne lege. Naprave ali telesa, ki nihajo, so nihala. V fiziki poznamo mehanska nihala in električne nihajne kroge.
V tem gradivu se bomo osredotočili na mehanska nihala. Primeri takih nihal so na sliki 1.

Slika 1: primeri mehanskih nihal: nihalo na vijačno vzmet, težno nihalo, nihala z vpetimi prožnimi jezički - glasbeni instrument, Newtonovo nihalo - kombinacija nihanja in trkov
Mehanska nihala so fizikalne naprave, kjer se potencialna ali prožnostna energija periodično pretvarjata v kinetično energijo nihajočega telesa in obratno. Iz tega izhajata dve osnovni vrsti nihal:
Prožnostno nihalo; primer prožnostnega nihala:
Težno nihalo; primer težnega nihala:
Nekatera mehanska nihala bomo spoznali tudi v drugih gradivih:
V tem gradivu bomo spoznali odgovore na naslednja vprašanja:
Kako telo niha?
Kako se med nihanjem spreminja energija telesa?
Kaj je vsiljeno nihanje in resonanca?
Kaj je dušeno nihanje?
Vzemimo primer nihanja, ki ga poznamo iz otroških let, gugalnico:
Opišimo sliko:
Otrok se vsede na stol gugalnice. Če ne deluje na njega nobena sila, obmiruje v najnižji legi. Imenujmo jo ravnovesno lego (položaj B na sliki 2).
Oče povleče otroka proti sebi tako, da doseže skrajno lego. V skrajni legi se otrok dvigne za višino h nad ravnovesno lego. Dobi potencialno energijo (položaj A na sliki 2).
Otroka spusti, le-ta zaniha. V spodnji (ravnovesni) legi ima največjo hitrost - največjo kinetično energijo, saj se je (skoraj) vsa potencialna energija pretvorila v kinetično.
Opazujemo oddaljevanje otroka od ravnovesne lege. V nekem trenutku je oddaljen od ravnovesne lege za y (položaj C na sliki 2). Ta razdalja se imenuje odmik od ravnovesne lege.
Hitrost (kinetična energija) se mu manjša, potencialna energija pa veča, dokler ne doseže nasprotno skrajno lego (položaj D na sliki 2). Razdaljo, ki jo naredi, imenujemo maksimalni odmik od ravnovesne lege ali amplituda. Označimo jo z 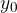 .
.
Od tega trenutna se giblje na enak način v nasprotno smer, dokler ne doseže prvotne lege.
Celotna pot, ki jo je opravil, dokler ni dosegel prvotne (začetne) lege, imenujemo en nihaj. Čas, ko je opravil en nihaj se imenuje nihajni čas 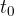 . Nasprotna vrednost nihajnemu času je lastna frekvenca nihanja
. Nasprotna vrednost nihajnemu času je lastna frekvenca nihanja 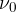 :
:
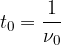
Nihanje se ponavlja.
Če otrok samo pasivno sedi na stolu in se ne odganja z nogami, nihanje postopno zamre. Vzrok za to je trenje v oseh gugalnice in upor zraka. Amplituda nihanja se manjša in končno pade na nič. Takšnemu nihanju pravimo dušeno nihanje.
Da nihanje prekmalu ne zamre, mu lahko pomaga oče tako, da ga vedno znova potisne, ko zaniha na njegovo stran. Dodaja mu kinetično energijo s katero nadomesti izgubljeno energijo zaradi trenja. Takšnemu nihanju pravimo vsiljeno nihanje. Če oče dodaja energijo v enakih časovnih intervalih, ki so enaki nihajnemu času, potem z najmanj dodane energije doseže največjo amplitudo nihanja otroka. Otrok v tem primeru niha z resonančno frekvenco.
Če je trenutna vrednost odklona telesa od ravnovesne lege sinusna funkcija časa, bo nihanje harmonično. V tem primeru veljajo vse formule in enačbe, ki smo jih izpeljali v gradivu Harmonično nihanje.
Realna nihala redko nihajo povsem harmonično. Še najbliže harmoničnemu nihanju je vzmetno nihalo, kjer velja Hookov zakon. Težno nihalo na splošno ne niha harmonično. Približno harmonično niha le pri dovolj majhnih amplitudah, kar lahko spoznamo v gradivu Matematično nihalo.
V gradivu Harmonično nihanje smo spoznali nekatere osnovne pojme in enačbe, ki valjajo za harmonično ali sinusno nihanje. Kako naredimo nihalo, ki bi niha harmonično in kako izračunamo njegov nihajni čas in frekvenco bomo spoznali v gradivih: Nihalo na vijačno vzmet, Nihalo na polžasto vzmet, Matematično nihalo in Fizično nihalo.
V poglavju Opis nihanja smo spoznali, da je nihanja v osnovi periodično (ponavljajoče) pretvarjanje energije iz ene oblike v drugo.
Da nihalo zanihamo, moramo premakniti telo iz ravnovesne lege za temenski odmik 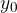 . Pri tem opravimo delo, damo pa mu potencialno ali prožnostno energijo. Ko telo spustimo, se prvotna energija zmanjšuje, kinetična enerija pa veča. Hitrost mu narašča in doseže največjo vrednost v ravnovesni legi, ko je vsa energija pretvori v kinetično. Proces se ponovi v obratni smeri: hitrost in s tem kinetična energija telesu pada in se na koncu pretvori v enako enerijo, kot je bila v začetku.
. Pri tem opravimo delo, damo pa mu potencialno ali prožnostno energijo. Ko telo spustimo, se prvotna energija zmanjšuje, kinetična enerija pa veča. Hitrost mu narašča in doseže največjo vrednost v ravnovesni legi, ko je vsa energija pretvori v kinetično. Proces se ponovi v obratni smeri: hitrost in s tem kinetična energija telesu pada in se na koncu pretvori v enako enerijo, kot je bila v začetku.
Velja, da je pri nedušenem nihanju vzmetnega nihala je vsota prožnostne in kinetične energije stalna pri vseh odmikih od ravnovesne lege. Enaka je maksimalni kinetični energiji ali maksimalni prožnostni energiji:
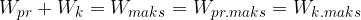
Pri nedušenem nihanju težnega nihala je vsota potencialne energije in kinetične energije stalna pri vseh odmikih od ravnovesne lege in je enaka maksimalni kinetični energiji ali maksimalni potencialni energiji:
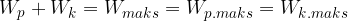
Pokažimo to trditev na vzmetnem nihalu.
Vzmetno nihalo je natančneje opisano v gradivu Nihalo na vijačno vzmet. Za naše trenutne potrebe vzemimo vzmetno nihalo v vodoravni legi. Na vzmet s konstanto k je pritrjena masa m, ki lahko brez trenja niha po vodoravno podlagi (glej sliko v gradivu Nihalo na vijačno vzmet).
Predpostavimo, da nihanje ni dušeno. Amplituda je konstantna.
Energija nihanja je v vsakem trenutku enaka vsoti prožnostne in kinetične energije:
Vsota prožnostne in kinetične energije nihala na vijačno vzmet je v vsakem trenutku enaka maksimalni energiji nihala.
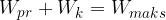
ali:
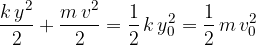
Zamislimo si nihalo v obliki enostransko vpetega jeklenega jezička (glej Stoječe transverzalno valovanje). Jeziček odmaknemo iz ravnovesne lege in spustimo tako, da zaniha z lastno frekvenve 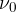 . Nihanje je dušeno, njegova amplituda postopno pade na nič.
. Nihanje je dušeno, njegova amplituda postopno pade na nič.
Pod jeklen jeziček damo zdaj elektromagnet in na njega priključimo generator izmenične napetosti. Elektromagnet s pomočjo izmeničnega magnetnega polja deluje s silo na jeziček tako, da zaniha z frekvenco, ki mu jo je vsilil generator - slika 4.
Če spremenimo frekvenco generatorja, spremenimo tudi frekvenco vsiljenega nihanja - s tem pa tudi amplitudo nihanja. Zanima nas naslednje:
kako se spreminja amplituda nihanja
v odvisnosti od frekvence?
To izvemo tako, da izmerimo amplitudo nihanja jezička pri različnih frekvencah in narišimo graf (glej sliko 5). Dobimo resonančno krivuljo nihala. Opazimo, da nihalo najmočneje zaniha takrat, ko je vsiljena frekvenca enaka lastni frekvenci nihala. Pravimo, da sta takrat sta generator in nihalo v resonanci.
Kolikšno amplitudo doseže nihalo v resonanci je odvisno od dušenja. Pri večjem dušenju je amplituda manjša (črtkana črta na sliki 5), pri manjšem dušenju pa večja (polna črta).
Zaradi trenja ali upora zraka se amplituda nihanja manjša, dokler ne pade na nič. Trenje in upor zraka opravljata namreč negativno delo, energija nihala se manjša. Nihanje je dušeno.
Predpostavimo, da je vzrok za dušenje upor zraka. V tem primeru se amplituda nihanja manjša po naslednji enačbi:
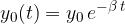
kjer je:
e naravno število 2,71,
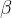 koeficient dušenja,
koeficient dušenja,
t čas,
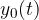 amplituda nihanja v nekem trenutku t,
amplituda nihanja v nekem trenutku t,
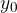 začetna amplituda nihanja.
začetna amplituda nihanja.
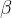 je enak obratni vrednosti tistega časa, ko se amplituda nihanja zmanjša za e-krat. Izračunajmo še, za kolikšen faktor pade tedaj amplituda (glej tudi sliko 6):
je enak obratni vrednosti tistega časa, ko se amplituda nihanja zmanjša za e-krat. Izračunajmo še, za kolikšen faktor pade tedaj amplituda (glej tudi sliko 6):
Zaradi dušenja se nihalu zmanjša tudi lastna frekvenca nihanja. Izpeljava izračuna lastne frekvence dušenega nihanja je zahtevnejša, zato podamo tu le rezultat:
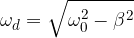
Iz enačbe lahko razberemo zanimivost in sicer, da lahko pade lastna frekvenca na nič. To se zgodi, ko je:
To je mejni primer, ko nihalo, potem ko ga spustimo, ne gre več skozi ravnovesno lego ampak se v ravnovesni legi ustavi. Pravimo, da je nihalo kritično dušeno (črtkana rdeča krivulja na sliki 6).
Pri dušenem nihanju pada amplituda nihanja po enačbi:
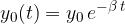
Pri tem je 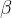 faktor dušenja. Enak je obratni vrednosti tistega časa, v katerem se amplituda nihanja zmanjša za e-krat.
faktor dušenja. Enak je obratni vrednosti tistega časa, v katerem se amplituda nihanja zmanjša za e-krat.
Zaradi dušenja se zniža tudi lastna frekvenca nihanja. Izračunamo jo lahko po enačbi:
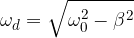
Nihalo je kritično dušeno, ko iz ene skrajne lege zaniha samo do ravnovesne lege (in ne zaniha okoli ravnovesne lege), nato pa se ustavi. Pogoj za kritično dušenje je: