Osebne zbirke


Naj bo dana krivulja 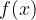 (zelene barve na sliki 1). In naj se linearna funkcija
(zelene barve na sliki 1). In naj se linearna funkcija 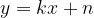 (rdeče barve na sliki 1) dotika funkcije
(rdeče barve na sliki 1) dotika funkcije 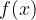 v točki T. Odvod funkcije
v točki T. Odvod funkcije 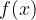 v točki T je enak natanko smernemu koeficientu linearne funkcije, k.
v točki T je enak natanko smernemu koeficientu linearne funkcije, k.
Odvod funkcije f v točki T(x,y) je smerni koeficient tangente na graf funkcije f v točki T(x,y).
Linearna premica, ki se dotika krivulje v eni točki je tangenta. Strmino tangente določa smerni koeficient, zato lahko poenostavljeno rečemo, da odvod določa strmino krivulje.
Iz teorije o linearni funkciji že vemo, kako se izračuna smerni koeficient:
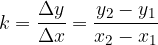
Za lažjo predstavo si izračun poglejmo še grafično:
Izračun smernega koeficienta k premice je neodvisen od izbire (dveh) točk, saj je za celo premico strmina enaka. Kaj se pa zgodi s smernim koeficientom, če obravnavamo krivulje, ki niso premice?
Za funkcije, ki niso premice, pa moramo razmišljanje o smernem koeficientu prilagoditi. Poglejmo si to grafično:
Tako kot pri premici, smo si tudi zdaj izbrali dve točki in na popolnoma enak način zapišemo enačbo za smerni koeficient:
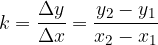
Opazimo, da pa se smerni koeficient spreminja, če spreminjamo točko:
Kako torej lahko dobimo smerni koeficient, ki ne bo odvisen od tega, kateri dve točki si izberemo?
Problem rešimo tako, da si izberemo dve točki, ki sta neskončno blizu. Poglejmo, kako to naredimo s pomočjo enačbe za smerni koeficient:
Dobili smo izraz za izračun odvoda! Z dosedanjim znanjem in definicijami, lahko definiramo odvod:
Kot smo že omenili lahko odvod definiramo kot:
Odvod funkcije v točki 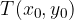 predstavlja smerni koeficient tangente na graf funkcije f v točki
predstavlja smerni koeficient tangente na graf funkcije f v točki 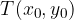 - to pa je limita diferenčnega kvocienta, ko gre h proti nič:
- to pa je limita diferenčnega kvocienta, ko gre h proti nič:
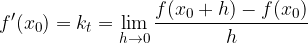
Računanje odvoda funkcije po definiciji je precej zamudno in ga uporabimo le v primeru, ko to naloga eksplicitno zahteva. Odvode računamo s pomočjo pravil in obrazcev, s katerimi se zelo poenostavi računanje odvodov tudi pri razmeroma precej kompliciranih funkcijah.
Za odvajanje izrazov z osnovnimi operacijami veljajo naslednja pravila:
Odvod funkcije pomnožene s konstanto
Zapišimo neko splošno funkcijo pomnoženo s konstanto:
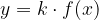
Ko y odvajamo, se konstanta prepiše, funkcija f(x) pa odvaja:
Odvod vsote oz. razlike dveh funkcij
Zapišimo neko splošno vsoto oziroma razliko:
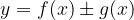
Odvod vsote / razlike je vsota / razlika odvodov:
Odvod produkta dveh funkcij
Zapišimo nek splošen produkt dveh (nekonstantnih) funkcij:
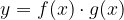
Odvod produkta dveh funkcij se izvede tako:
Odvod količnika dveh funkcij
Zapišimo nek splošen kvocient dveh (nekonstantnih) funkcij:
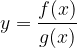
Odvod kvocienta dveh funkcij se izvede tako:
Sedaj si poglejmo še obrazce za odvajanje:
Odvajanje je dosti lažje, če poznamo odvode pogosto ponavljajočih se funkcij kar na pamet. Poglejmo si odvode funkcij, ki jih v matematiki pogosto srečujemo:
Poglejmo si še enkrat sliko:
in zapišimo smerni koeficient premice:
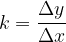
Opazimo, da smerni koeficient nič drugega kot tangens kota 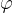 :
:
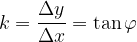
Pri obravnavanju tangente na krivuljo smo po drugi strani ugotovili, da je smerni koeficient tangente na funkcijo f(x) v konkretni točki 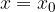 enak odvodu funkcije v tej točki:
enak odvodu funkcije v tej točki:
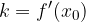
Posledično lahko zapišemo geometrični pomen odvoda, ki je:
Odvod funkcije je smerni koeficient tangente na krivuljo v dani točki in ta je enak tangensu naklonskega kota, ki ga tangenta oklepa s pozitivno smerjo osi x: