Osebne zbirke


Vsaka funkcija ima svoj osnovni predpis, ki določa njene lastnosti in obliko grafa.
Če osnovni predpis preoblikujemo, se funkcija spremeni, z njo pa tudi lega, oblika ali simetrija grafa funkcije.
V nadaljevanju si bomo podrobno ogledali operacije, ki jih lahko izvajamo nad funkcijami.
Tako kot geometrijske like v ravnini lahko transformiramo tudi funkcije. Transformacije si najlažje ogledamo na grafu funkcije.
Funkcijo vzporedno premaknemo tako, da:
neodvisni spremenljivki 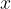 ali
ali
vrednosti funkcije 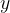
dodamo ali pa odvzamemo konstantno vrednost.
Graf funkcije se s tem premakne po koordinatnem sistemu podobno kot geometrijski lik: levo, desno, gor ali dol, a brez spremembe oblike.
Če funkciji  dodamo število
dodamo število 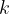 , se njen graf:
, se njen graf:
premakne navzgor, če 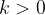 oziroma
oziroma
premakne navzdol, če 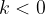 .
.
Če neodvisni spremenljivki 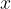 funkcije
funkcije  dodamo število
dodamo število 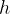 , se njen graf:
, se njen graf:
premakne levo, če 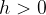 oziroma
oziroma
premakne desno, če 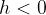 .
.
Če obstajata funkcija  in števili
in števili 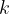 in
in 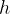 , za kateri velja
, za kateri velja 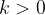 in
in 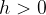 , potem bo funkcija:
, potem bo funkcija:
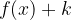 premaknjena navzgor glede na osnovno funkcijo
premaknjena navzgor glede na osnovno funkcijo  ,
,
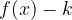 premaknjena navzdol glede na osnovno funkcijo
premaknjena navzdol glede na osnovno funkcijo  ,
,
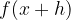 premaknjena levo glede na osnovno funkcijo
premaknjena levo glede na osnovno funkcijo  in
in
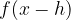 premaknjena desno glede na osnovno funkcijo
premaknjena desno glede na osnovno funkcijo  .
.
Pri raztegu se graf funkcije razširi ali skrči, ne da bi spremenil svojo osnovno obliko.
Če funkcijo  pomnožimo s poljubnim številom
pomnožimo s poljubnim številom 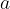 , se njen graf:
, se njen graf:
vertikalno raztegne, če je število 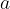 večje od 1 oziroma
večje od 1 oziroma
vertikalno skrči, če je vrednost števila 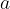 med 0 in 1.
med 0 in 1.
Če obstaja funkcija  in pozitivno realno število
in pozitivno realno število 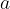 , je funkcija
, je funkcija  :
:
vertikalno raztegnjena napram osnovni funkciji  , če
, če 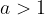 oziroma
oziroma
vertikalno skrčena napram osnovni funkciji  , če
, če 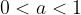 .
.
Če neodvisno spremenljivko 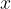 funkcije
funkcije  pomnožimo s poljubnim številom
pomnožimo s poljubnim številom 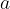 , se njen graf:
, se njen graf:
horizontalno skrči, če je število 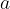 večje od 1 oziroma
večje od 1 oziroma
horizontalno raztegne, če je vrednost števila 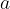 med 0 in 1.
med 0 in 1.
Če obstaja funkcija  in pozitivno realno število
in pozitivno realno število 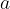 , je funkcija
, je funkcija 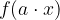 :
:
vertikalno raztegnjena napram osnovni funkciji  , če
, če 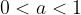 oziroma
oziroma
vertikalno skrčena napram osnovni funkciji  , če
, če 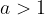 .
.
Pri zrcaljenju se graf funkcije obrne preko osi 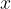 ali preko osi
ali preko osi 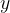 .
.
Če funkcijo  pomnožimo s številom -1, se vse zaloge vrednosti zamenjajo z nasprotnimi vrednostmi. Vsaka pozitivna vrednost postane negativna in obratno. Edino ničla funkcije ostane nespremenjena.
pomnožimo s številom -1, se vse zaloge vrednosti zamenjajo z nasprotnimi vrednostmi. Vsaka pozitivna vrednost postane negativna in obratno. Edino ničla funkcije ostane nespremenjena.
Graf take funkcije je čez os 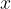 prezrcaljena slika grafa osnovne funkcije.
prezrcaljena slika grafa osnovne funkcije.
Če neodvisno spremenljivko 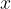 funkcije
funkcije  pomnožimo s številom -1, potem bodo vrednosti funkcije pri pozitivnih
pomnožimo s številom -1, potem bodo vrednosti funkcije pri pozitivnih 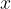 -ih zamenjane s tistimi vrednostmi od negativnih
-ih zamenjane s tistimi vrednostmi od negativnih 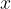 -ov.
-ov.
Graf take funkcije je čez os 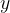 prezrcaljena slika grafa osnovne funkcije.
prezrcaljena slika grafa osnovne funkcije.
Grafa funkcij  in
in 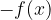 sta zrcalna glede na
sta zrcalna glede na 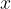 os.
os.
Grafa funkcij  in
in 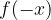 sta zrcalna glede na
sta zrcalna glede na 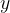 os.
os.
Absolutna vrednost funkcije  ima povsod pozitivne vrednosti. Zapišemo jo:
ima povsod pozitivne vrednosti. Zapišemo jo:

Če imamo že narisan graf funkcije  , potem graf absolutne vrednosti funkcije dobimo tako, da del, ki se nahaja pod osjo
, potem graf absolutne vrednosti funkcije dobimo tako, da del, ki se nahaja pod osjo 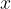 , preslikamo čez os
, preslikamo čez os 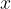 .
.
Inverzna funkcija je predpis, ki za dano funkcijo  obrne proces preslikave, tako da vsako vrednost
obrne proces preslikave, tako da vsako vrednost  preslika nazaj v original
preslika nazaj v original 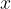 :
:
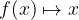
Z drugimi besedami, če funkcija 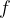 preslika
preslika 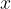 v
v 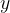 , potem inverzna funkcija
, potem inverzna funkcija 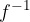 preslika
preslika 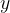 nazaj v
nazaj v 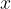 .
.
Pri tem je pomembno poudariti, da inverzna funkcija obstaja le za bijektivne funkcije. Če celotna funkcija ni bijektivna, potem lahko določimo inverz samo na intervalu, kjer je funkcija bijektivna. Poglejmo, zakaj je tako.
Bijektivna funkcija je hkrati:
surjektivna (vsak element iz zaloge vrednosti je slika nekega elementa iz definicijskega območja),
in injektivna (vsak element iz definicijskega območja se preslika v različen element zaloge vrednosti).
Surjektivnost nam zagotavlja, da funkcija pokrije celotno zalogo vrednosti, injektivnost pa zagotavlja enoličnost preslikave, zato lahko iz vsake slike pridemo nazaj do natančno enega originala.
Predpis za inverzno funkcijo dobimo tako, da:
neodvisno spremenljivko 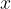 zamenjamo z odvisno spremenljivko
zamenjamo z odvisno spremenljivko 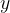 in obratno,
in obratno,
nato pa izrazimo 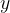 .
.
Originalna in inverzna funkcija imata med seboj zamenjani tudi definicijsko območje in zalogo vrednosti.
Za vsak 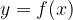 iz zaloge vrednosti funkcije
iz zaloge vrednosti funkcije  velja
velja
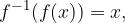
pri čemer je 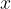 element definicijskega območja funkcije
element definicijskega območja funkcije  .
.
Graf inverzne funkcije lahko narišemo tudi brez iskanja predpisa inverzne funkcije. Na hitro ga dobimo tako, da prvotno funkcijo prezrcalimo preko simetrale lihih kvadrantov, ki jo predstavlja premica 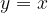 .
.
Tako funkcijo najlažje prepoznamo po njenem grafu, ki je sestavljen iz več delov.
Poseben primer takih funkcij so stopničaste funkcije, ki imajo na posameznih intervalih konstantne vrednosti, zato njihov graf izgleda kot stopnice.
Odsekoma definirane funkcije imajo več predpisov, od katerih vsak velja na svojem intervalu definicijskega območja.
Graf take funkcije najenostavneje narišemo tako, da najprej v isti koordinatni sistem narišemo grafe za vse predpise, nato pa posamezen graf poudarimo na intervalu, kjer je definiran.
Do sedaj smo si ogledali operacije nad eno samo funkcijo, v nadaljevanju pa poglejmo še operacije nad dvema funkcijama, ki jih lahko razširimo tudi na več funkcij.
Funkcije lahko seštevamo, odštevamo, množimo, delimo ali sestavljamo skupaj.
Sestavljeno funkcijo (ali kompozitum funkcij) dobimo tako, da izhod ene funkcije uporabimo kot vhod v drugo funkcijo.
Imejmo funkciji  in
in 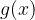 . Sestavimo funkcijo, ki namesto spremenljivke vzame drugo funkcijo:
. Sestavimo funkcijo, ki namesto spremenljivke vzame drugo funkcijo:
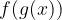
Če je tako sestavljena funkcija definirana, potem jo enostavneje zapišemo s krožcem. Tak zapis običajno imenujemo kompozitum funkcij:

Naj bosta 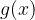 in
in 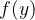 funkciji, za kateri velja:
funkciji, za kateri velja:
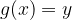 in
in
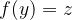
Spremenljivka 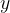 je torej hkrati odvisna spremenljivka funkcije
je torej hkrati odvisna spremenljivka funkcije 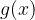 in neodvisna spremenljivka funkcije
in neodvisna spremenljivka funkcije 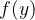 .
.
Kompozitum funkcij v matematičnem jeziku zapišemo kot
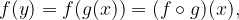
kjer rezultat funkcije 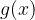 predstavlja vhod funkcije
predstavlja vhod funkcije 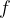 .
.
Vsako točko 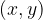 grafa sestavljene funkcije bi lahko posebej izračunali, tako da:
grafa sestavljene funkcije bi lahko posebej izračunali, tako da:
najprej vzamemo poljubno točko 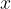 in s tem dobimo prvo koordinato točke,
in s tem dobimo prvo koordinato točke,
izračunamo vrednost 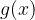 in
in
potem pa dobljeno vrednost še enkrat preračunamo s predpisom  in tako dobimo koordinato
in tako dobimo koordinato 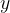 točke na grafu.
točke na grafu.
Ni pa potrebno risati vsake točke posebej. Hitrejši smo, če graf sestavljene funkcije 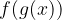 s transformacijami grafov:
s transformacijami grafov:
najprej narišemo graf notranje funkcije 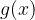 ,
,
nato upoštevamo še transformacije funkcije  .
.
Rezultat je graf sestavljene funkcije 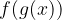 .
.