Prijava z e-naslovom
Prijava brez gesla
O transverzalnem valovanju govorimo, ko se delci gibljejo pravokotno na smer gibanja valovanja. Primer transverzalnega vala je npr. val na dolgi napeti vrvi, ki jo na eni strani zanihamo z roko. Motnja se širi vzdolž vrvi medtem ko delci vrvi zanihajo pravokotno na vrv, kot kaže slika.
Slika 1: Motnja se širi vzdolž vrvi, delci nihajo pravokotno.
Sinusno transverzalno valovanje dobimo, če vzbujamo začetek vrvi po sinusni funkciji časa. Val, ki nastane na vrvi v nekem trenutku opazovanja (naj bo ta trenutek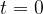 
), zgleda tako, kot kaže slika:
Slika 2: Transverzalni val v času t = 0.
Val na sliki 2 pa ne miruje, pač pa potuje vzdolž osi x s hitrostjo c. Če bi opazovali samo en delček vrvi na neki razdalji x od začetka, bi videli, da ta delček niha sinusno v smeri y osi z neko periodo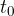 
, frekvenco 
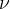in amplitudo 
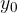(našteti pojmi so opisani v poglavju Harmonično nihanje).
Predno preidemo na matematični zapis enačb, najprej zapišimo osnovne pojme transverzalnega valovanja. Naštete pojme bomo kasneje natančno razložili.
Harmonično ali sinusno transverzalno valovanje je valovanje, kjer nihajo delci pravokotno na smer širjenja valovanja in se lahko opiše njihov odmik od ravnovesne lege y kot sinusna funkcija razdalje in časa.
Amplituda transverzalnega valovanja 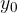je maksimalni ali temenski odmik vala od ravnovesne lege (od osi x na sliki 2). Maksimalni odmik imenujemo tudi greben vala (hrib) in v nasprotni smeri dolina vala.
Perioda je čas, ko si v opazovani razdalji x sledita dva grebena ali dve dolini vala. (Pojem perioda ima isti pomen ko obhodni čas pri kroženju ali nihajni čas pri nihanju).
Valovna dolžina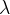 
je dolžina enega vala, npr: razdalja med dvema grebenoma ali pa dolinama vala.
Frekvenca valovanja 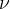je recipročna vrednost periode. Pove, kolikokrat na sekundo val zaniha.
Hitrost vala označimo s c. Val se enakomerno giblje vzdolž osi x, torej v smeri, ki je pravokotna na nihanje delcev.
Vrv na sliki 1 vzbujajmo npr. s stalnim sinusnim nihanjem roke. Odmik vrvi od ravnovesne lege lahko zato opišemo z isto enačbo, kot smo jo spoznali v poglavju Harmonično nihanje:
Nihaji, ki jih povzročamo na začetku vrvi, se širijo vzdolž vrvi z enakomerno hitrostjo c. Velja enaka enačba za pot kot pri enakomernem gibanju: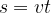 
. Oziroma, v tem primeru, pot ali razdalja ene valovne dolžine 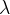je enaka produktu med:
hitrostjo širjenja valovanja c in
hitrostjo širjenja valovanja in časa ene periode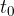 
.
Zapišimo enačbo:
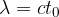
Z upoštevanjem povezanosti frekvence 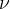in časa ene periode :
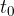dobimo:
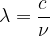
ali
Frekvenca in valovna dolžina sta obratno sorazmerni. Povezuje ju hitrost valovanja c:
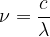
Opisali smo potujoče transverzalno valovanje. Vrv niha prečno, val pa se širi vzdolžno po vrvi. Trenutni odmik vrvi od ravnovesne lege v razdalji x od začetka vrvi bo odvisen od časa t in razdalje x.
Z enačbo:
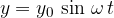
lahko določimo:
odmik od ravnovesne lege y za poljubni čas na izhodiščni legi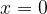 
,
ali pa, če t nadomestimo s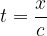 
:
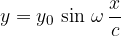
odmik od ravnovesne lege y za katerikoli kraj v času .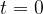
Radi pa bi enačbo, s katero bi lahko določili odmik od ravnovesne lege:
v kateremkoli času
za katerikoli kraj hkrati.
Tako enačbo izpeljemo tako, da si najprej zamislimo val, ki se je premaknil (glej sliko 3). V času t, se je val premaknil za:
Slika 3: Potujoči val.
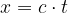
Z našo enačbo poskušajmo slediti točki, ki ni odmaknjena od ravnovesne lege. Očitno lahko to storimo z enačbo:
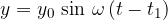
Preverimo: če v enačbo vstavimo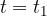 
, je argument funkcije sinus enak 0 in amplituda je tudi 0 - tako kot mora biti. Enačba nam že omogoča, da si izberemo poljuben trenutek valovanja 
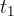. Ker pa si želimo hkrati še izbrati poljubno koordinato x, koordinato x vpeljemo prek časa .
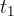Izpeljimo:
Argument sinusa v zgornji enačbi ima dva člena:
prvi predstavlja odvisnost odmika ravnovesne lege od časa t,
drugi pa od razdalje x.
Če postavimo v enačbi 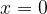, dobimo odvisnost od časa (glej sliko 4 levo):
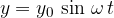
Če postavimo v enačbi 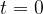, dobimo odvisnost od razdalje (glej sliko 4 desno):
Slika 4: graf odvisnosti potujočega vala od časa (levo) in od razdalje (desno).
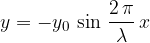
Enačba za potujoči transverzalni val je:
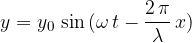
kjer je t poljuben trenutek valovanja, x pa poljubna koordinata valovanja.
Hitrost valovanja na napeti vrvi ali struni računamo po enačbi:
Tu je gostota snovi:
in natezna napetost:
Izpeljimo še drugo obliko za izračun hitrosti valovanja. V enačbo (4) vstavimo enačbi (5) in (6):
