Osebne zbirke


Bicikel obrnemo na glavo tako, da stoji na balanci in sedežu. Primemo sprednje kolo in ga s sunkom roke zavrtimo. Kolo je na začetku mirovalo, po delovanje sunka sile naših rok pa se je vrtelo z določeno kotno hitrostjo. V času delovanja sile so se vse točke na obodu gibale enakomerno pospešeno.
Če bi prijeli kolo namesto na obodu raje na špici nekoliko bliže osi vrtenja (glej sliko 1), bi za isto končno kotno hitrost potrebovali nekoliko večjo silo. To nam da misliti, da smo za določeno hitrost vrtenja kolesa potrebovali navor sile. Navor smo povzročili s silo naših rok; pri tem je ročica enaka razdalji med silo in osjo vrtenja.
Z navorom M, s katerim na sistem delujemo določen čas 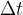 , smo kolesu spremenili hitrost kroženja. Pravimo, da smo s sunkom navora M spremenili vrtilno količino, ki jo označimo z grško črko gama:
, smo kolesu spremenili hitrost kroženja. Pravimo, da smo s sunkom navora M spremenili vrtilno količino, ki jo označimo z grško črko gama:
V tem poglavju bomo spoznali dve novi fizikalni veličini, ki sta tesno povezani z vrtilno količino:
vztrajnostni moment,
vrtilno količino.
Podoben pomen kot ga ima masa pri gibalni količini, ima vztrajnostni moment pri vrtilni količini. Zaradi mase telo vztraja v gibanju, če na njega ne deluje nobena sila. Podobno velja za vztrajnostni moment pri kroženju: telo vztraja pri kroženju, če na njega ne deluje noben navor.
Spoznajmo najprej vztrajnostni moment točkastega telesa, ki kroži po krožnici z radijem r. Znanje iz tega preprostega primera nato razširimo na vrteče se togo telo.
Na točkasto telo, ki kroži enakomerno pospešeno, delujeta dve sili (slika 2):
Radialna sila 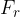 je sila, ki sili telo v kroženje. Je enaka produktu mase in radialnega pospeška:
je sila, ki sili telo v kroženje. Je enaka produktu mase in radialnega pospeška:
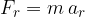
kjer je radialni pospešek:
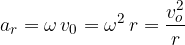
Ker se obodna hitrost spreminja s časom (telo enakomerno pospešeno kroži), se tudi radialni pospešek spreminja s časom. Če obodna hitrost narašča, narašča tudi radialni pospešek.
Druga sila je tangencialna sila 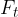 . V skladu z 2. Newtonovim zakonom povzroči, da se telo giblje z obodnim pospeškom
. V skladu z 2. Newtonovim zakonom povzroči, da se telo giblje z obodnim pospeškom 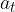 :
:
Izraze, ki smo jih dobili, imenujemo tudi 2. Newtonov zakon za kroženje. Zapišimo povezavo med silo in pospeškom (2. Newtonov zakon):
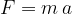
Nadomestimo silo F z navorom M, maso m z vztrajnostnim momentom J in pospešek a s kotnim pospeškom 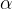 in dobimo:
in dobimo:
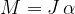
Navor sile na vrteče točkasto telo povzroči, da se telo giblje s kotnim pospeškom 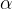 . Faktor sorazmernosti je vztrajnostni moment J:
. Faktor sorazmernosti je vztrajnostni moment J:
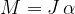
Pri tem je kotni pospešek količnik med tangencialnim pospeškom in radijem:
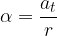
Vztrajnostni moment točkastega telesa pa je:
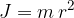
Vzemimo poljubno togo telo, ki se vrti okoli poljubne osi, kot kaže slika 3.
Telo razdelimo na n majhnih kvadrov z maso 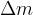 . Kvadri so oddaljeni od rotacijske osi za različne razdalje r.
. Kvadri so oddaljeni od rotacijske osi za različne razdalje r.
Prvi kvader ima svoj vztrajnostni moment:
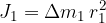
drugi kvader:
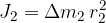
poljubni i-ti kvader pa:
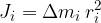
Vztrajnostni moment celotnega telesa je enak vsoti vztrajnostnih momentov posameznih delov:
Vztrajnostni moment togega telesa je vsota vztrajnostnih momentov delov telesa pri podani osi vrtenja:
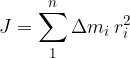
Zapišimo še vztrajnostne momente nekaterih drugih geometrijskih teles:
Že v uvodu smo omenili, da navor, ki traja določen čas 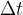 , spremeni vrtilno količino telesa. Nismo pa povedali, kaj je vrtilna količina.
, spremeni vrtilno količino telesa. Nismo pa povedali, kaj je vrtilna količina.
Zapišimo še enkrat povezavo med navorom M, vztrajnostnim momentom J in kotnim pospeškom 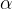 :
:
Definirali smo vrtilno količino kot produkt vztrajnostnega momenta in kotne hitrosti:
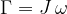
Vrtilna količina je vektor. Mi ga bomo zapisali kot skalar, pri čemer bomo upoštevali predznak:
Vrtenje v obratni smeri urinega kazalca da pozitivno vrtilno količino.
Vrtenje v smeri urinega kazalca pa da negativno vrtilno količino.
Vrtilna količina je produkt vztrajnostnega momenta in kotne hitrosti:
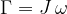
Vrtilna količina je pozitivna, če se telo vrti v obratni smeri urinega kazalca in negativna, če se vrti v smeri urinega kazalca.
Vrtilna količina in gibalna količina sta si sorodna pojma in se dopolnjujeta. Če gibalno količino računamo telesom, ki se gibljejo translacijsko (npr. po premici), vrtilno količino računamo telesom, ki se vrtijo okoli dane osi.
Zapišimo še enkrat izraz:
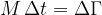
Izraz na levi strani pomeni sunek navora, na desni pa spremembo vrtilne količine:
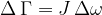
Zapisan izraz se imenuje izrek o vrtilni količini.
Če delujemo na telo, ki se lahko vrti okoli izbrane osi s sunkom navora, mu spremenimo vrtilno količino.
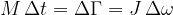
Če ni zunanjega sunka navora, se vrtilna količina ohrani:
Če ni zunanjega sunka navora, se vrtilna količina ohrani:
