Prijava z e-naslovom
Prijava brez gesla
Deltoid konstruiramo na podlagi poznavanja konstrukcije osnovnih geometrijskih elementov, kotov in preslikav.
Za konstrukcijo paralelograma potrebujemo tri neodvisne podatke. Ti podatki so kombinacija:
stranic
notranjih kotov in
diagonal
Pred vsako konstrukcijo paralelograma narišemo skico, ki nam služi za orientacijo pri risanju. Na skici po možnosti označimo vsak podatek s svojo barvo.
V nadaljevanju so opisani koraki konstrukcije za različne kombinacije podatkov. Navedena sta tudi pogoja za izvedbo konstrukcije.
Pogoja za izvedbo konstrukcije
Prvi pogoj (pogoj za velikost podanih kotov):
Drugi pogoj (trikotniška neenakost):
V trikotniku, ki ga sestavljajo stranici in diagonala deltoida, mora biti zadoščen pogoj trikotniške neenakosti.
Zgornji pogoj velja za naslednje trikotnike znotraj deltoida:
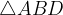
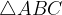
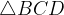
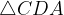
Pogoja veljata za vse spodaj navedene konstrukcije.
Možni so trije načini tovrstnega podajanja stranic in kota:
V nadaljevanju so opisani koraki za prvo kombinacijo iz zgornje tabele.
Pri podajanju vrednosti je potrebno upoštevati prvi pogoj za izvedbo konstrukcije.
Skica
Pri konstrukciji upoštevamo, da je deltoid osno simetričen lik, katerega simetrala poteka skozi točki B in D. Omenjeno lastnost upoštevamo v četrtem koraku konstrukcije.
1. korak
Z ravnilom narišemo daljico dolžine a. Končni točki daljice označimo z A in B.
2. korak
Konstruiramo kot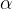 
z vrhom v točki A. Prvi krak kota 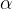je usmerjen navzdol in sovpada z nosilko daljice AB, drugi krak pa je usmerjen navzgor proti oglišču D deltoida (glej skico).
3. korak
V šestilo vzamemo dolžino stranice b.
Šestilo zapičimo v točko A.
S šestilom zarišemo krožni lok v smeri proti oglišču D deltoida (glej skico), tako da seka krak kota 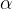. Tako nastalo presečišče označimo s točko D:
Koraki 1, 2 in 3
Daljica AB predstavlja stranico a, daljica AD pa stranico b deltoida. A, B in D so tri izmed štirih oglišč deltoida.
4. korak
Z ravnilom narišemo premico skozi točki B in D ter jo označimo z s. Premica s predstavlja simetralo deltoida.
Vsa narisana oglišča in stranice preslikamo čez simetralo s:
oglišči B in D se preslikata sami vase,
slika oglišča A predstavlja oglišče C, tj. četrto oglišče deltoida,
stranici a in b se preslikata v sebi skladni stranici; označimo ju prav tako z a in b:
Korak 4
Možnih je šest načinov tovrstnega podajanja stranice in kotov:
V nadaljevanju so opisani koraki za prvo kombinacijo iz zgornje tabele.
Pri podajanju vrednosti je potrebno upoštevati prvi pogoj za izvedbo konstrukcije.
Skica
1. korak
Narišemo daljico dolžine a. Končni točki daljice označimo z A in B.
2. korak
Konstruiramo kot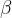 
z vrhom v točki B. Levi krak kota 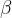sovpada z nosilko daljice AB, desni krak pa je usmerjen proti oglišču C deltoida (glej skico).
3. korak
V šestilo vzamemo dolžino stranice a.
Šestilo zapičimo v točko B.
S šestilom zarišemo krožni lok v smeri proti oglišču C deltoida (glej skico), tako da seka krak kota 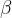. Tako nastalo presečišče označimo s točko C:
Koraki 1, 2 in 3
Daljica AB predstavlja je prva iz para skladnih stranic dolžine a. A, B in C so tri izmed štirih oglišč deltoida.
4. korak
Poudarimo daljico BC.
5. korak
Konstruiramo simetralo kota 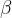in jo označimo z 
.
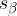6. korak
Konstruiramo kot 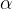z vrhom v točki A. Prvi krak kota 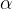je usmerjen navzdol in sovpada z nosilko daljice AB, drugi krak pa je usmerjen navzgor proti oglišču D deltoida (glej skico).
Točko, kjer zgornji krak kota 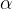seka simetralo 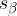, označimo z D:
Koraki 4, 5 in 6
Daljica BC je druga iz para skladnih stranic dolžine a, D pa je četrto oglišče deltoida.
7. korak
Z ravnilom povežemo točki C in D ter poudarimo daljico AD:
Korak 7
Daljici CD in AD predstavljata par skladnih stranic dolžine b.
Možna sta dva načina tovrstnega podajanja stranic in kota:
V nadaljevanju so opisani koraki za drugo kombinacijo iz zgornje tabele.
Pri podajanju vrednosti je potrebno upoštevati drugi pogoj za izvedbo konstrukcije.
Skica
Pri konstrukciji upoštevamo, da je deltoid osno simetričen lik, katerega simetrala poteka skozi točki B in D. Omenjeno lastnost upoštevamo v petem koraku konstrukcije.
1. korak
Z ravnilom narišemo navpično daljico dolžine f. Končni točki daljice označimo z B in D.
2. korak
V šestilo vzamemo dolžino stranice a.
Šestilo zapičimo v točko B.
S šestilom zarišemo krožni lok v smeri proti oglišču A deltoida (glej skico).
3. korak
V šestilo vzamemo dolžino stranice b.
Šestilo zapičimo v točko D.
S šestilom zarišemo krožni lok tako, da seka predhodno narisan krožni lok. Presečišče krožnih lokov označimo s točko A:
Koraki 1, 2 in 3
Točke A, B in D predstavljajo tri izmed štirih oglišč deltoida. Daljica f je diagonala deltoida.
4. korak
Z ravnilom povežemo točki A in B ter točki A in D:
Korak 4
Daljica AB predstavlja stranico a, daljica AD pa stranico b deltoida.
5. korak
Z ravnilom narišemo simetralo daljice BD ter jo označimo z s. Premica s predstavlja simetralo deltoida.
Vsa narisana oglišča in stranice preslikamo čez simetralo s:
oglišči B in D se preslikata sami vase,
slika oglišča A predstavlja oglišče C, tj. četrto oglišče deltoida,
stranici a in b se preslikata v sebi skladni stranici; označimo ju prav tako z a in b:
Korak 5
Možna sta dva načina tovrstnega podajanja stranice in diagonal:
V nadaljevanju so opisani koraki za prvo kombinacijo iz zgornje tabele.
Pri podajanju vrednosti je potrebno upoštevati drugi pogoj za izvedbo konstrukcije.
Skica
1. korak
Z ravnilom narišemo vodoravno daljico dolžine e. Končni točki daljice označimo z A in C.
2. korak
Konstruiramo razpolovišče daljice AC in ga označimo s točko E.
3. korak
V šestilo vzamemo dolžino stranice a.
Šestilo zapičimo v točko A.
S šestilom zarišemo krožni lok v smeri proti oglišču B deltoida (glej skico).
Šestilo zapičimo v točko C.
S šestilom zarišemo krožni lok tako, da seka predhodno narisan krožni lok. Presečišče krožnih lokov označimo s točko B:
Koraki 1, 2 in 3
Točke A, B in C predstavljajo tri izmed štirih oglišč deltoida.
4. korak
Z ravnilom povežemo točki A in B ter točki B in C.
5. korak
Z ravnilom narišemo premico skozi točki B in E ter jo označimo z s.
6. korak
V šestilo vzamemo dolžino diagonale f.
Šestilo zapičimo v točko A.
S šestilom zarišemo krožni lok v smeri proti oglišču D deltoida (glej skico), tako da seka premico s. Tako nastalo presečišče označimo s točko D:
Koraki 4, 5 in 6
Daljici AB in BC predstavljata par skladnih stranic dolžine a, D pa je četrto oglišče deltoida.
7. korak
Z ravnilom povežemo točki C in D ter točki A in D:
Koraki 4, 5 in 6
Daljici CD in AD predstavljata par skladnih stranic dolžine b.
Premica s predstavlja simetralo deltoida.
Možnih je šest načinov tovrstnega podajanja kotov in diagonale:
V nadaljevanju so opisani koraki za peto kombinacijo iz zgornje tabele.
Pri podajanju vrednosti je potrebno upoštevati prvi pogoj za izvedbo konstrukcije.
Skica
Pri konstrukciji upoštevamo, da je deltoid osno simetričen lik, katerega simetrala poteka skozi točki B in D. Omenjeno lastnost upoštevamo v petem koraku konstrukcije.
1. korak
Z ravnilom narišemo navpično daljico dolžine f. Končni točki daljice označimo z B in D.
2. korak
Konstruiramo kot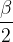 
z vrhom v točki B. Poševni krak kota 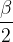je usmerjen proti oglišču A deltoida (glej skico), navpični krak pa sovpada z nosilko daljice BD.
3. korak
Konstruiramo kot 
z vrhom v točki D. Poševni krak kota je usmerjen proti oglišču A deltoida (glej skico), navpični krak pa sovpada z nosilko daljice BD.
Presečišče poševnih krakov kotov 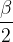in označimo s točko A:
Koraki 1, 2 in 3
Točke A, B in D predstavljajo tri izmed štirih oglišč deltoida.
4. korak
Poudarimo daljici AB in AD.
Korak 4
Daljica AB predstavlja stranico a, daljica AD pa stranico b deltoida.
5. korak
Z ravnilom narišemo simetralo daljice BD ter jo označimo z s. Premica s predstavlja simetralo deltoida.
Vsa narisana oglišča in stranice preslikamo čez simetralo s:
oglišči B in D se preslikata sami vase,
slika oglišča A predstavlja oglišče C, tj. četrto oglišče deltoida,
stranici a in b se preslikata v sebi skladni stranici; označimo ju prav tako z a in b:
Korak 5
Možna sta dva načina tovrstnega podajanja kota in diagonal:
V nadaljevanju so opisani koraki za prvo kombinacijo iz zgornje tabele.
Pri podajanju vrednosti je potrebno upoštevati prvi pogoj za izvedbo konstrukcije.
Skica
Pri konstrukciji upoštevamo, da je deltoid osno simetričen lik, katerega simetrala sovpada s simetralo kota 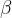. Omenjeno lastnost upoštevamo v šestem koraku konstrukcije.
1. korak
Konstruiramo kot 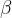z vrhom v točki B. Levi krak kota 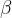je usmerjen proti oglišču A, desni krak pa je usmerjen proti oglišču C deltoida (glej skico).
2. korak
Konstruiramo simetralo kota 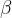in jo označimo z .
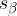3. korak
V šestilo vzamemo dolžino diagonale f.
Šestilo zapičimo v točko B.
S šestilom zarišemo krožni lok v smeri proti oglišču D deltoida (glej skico), tako da seka simetralo 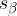. Tako nastalo presečišče označimo s točko D:
Koraki 1, 2 in 3
Točki B in D predstavljata dve izmed štirih oglišč deltoida.
4. korak
Konstruiramo vzporednico simetrali 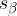na razdalji 
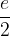levo od simetrale in jo označimo s p.
Presečišče premice p in levega kraka kota 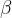označimo s točko A:
Korak 4
Točka A predstavlja tretje oglišče, f pa je diagonala deltoida.
5. korak
Z ravnilom povežemo točki A in D ter poudarimo daljico AB:
Korak 5
Daljica AB predstavlja stranico a, daljica AD pa stranico b deltoida. 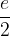predstavlja polovico diagonale e.
6. korak
Upoštevamo, da je 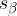simetrala deltoida in čez njo preslikamo vsa narisane točke in daljice
oglišči B in D in kot 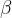se preslikajo sami vase,
slika oglišča A predstavlja oglišče C, tj. četrto oglišče deltoida,
stranici a in b se preslikata v sebi skladni stranici; označimo ju prav tako z a in b
Polovica diagonale 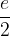se preslika v drugo polovico le-te:
Korak 6
Možnih je dvanajst načinov tovrstnega podajanja stranice in kotov:
V nadaljevanju so opisani koraki za prvo kombinacijo iz zgornje tabele.
Pri podajanju vrednosti je potrebno upoštevati prvi in drugi pogoj za izvedbo konstrukcije.
Skica
1. korak
Z ravnilom narišemo vodoravno daljico dolžine e. Končni točki daljice označimo z A in C.
2. korak
Konstruiramo razpolovišče daljice AC in ga označimo s točko E.
3. korak
V šestilo vzamemo dolžino stranice a.
Šestilo zapičimo v točko A.
S šestilom zarišemo krožni lok v smeri proti oglišču B deltoida (glej skico).
Šestilo zapičimo v točko C.
S šestilom zarišemo krožni lok tako, da seka predhodno narisan krožni lok. Presečišče krožnih lokov označimo s točko B:
Koraki 1, 2 in 3
Točke A, B in C predstavljajo tri izmed štirih oglišč deltoida.
4. korak
Z ravnilom povežemo točki A in B ter točki B in C.
5. korak
Z ravnilom narišemo premico skozi točki B in E ter jo označimo z s.
6. korak
Konstruiramo kot 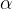z vrhom v točki A. Prvi krak kota 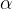je usmerjen navzdol in sovpada z nosilko daljice AB, drugi krak pa je usmerjen navzgor proti oglišču D deltoida (glej skico).
Točko, kjer zgornji krak kota 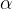seka simetralo s, označimo z D:
Koraki 4, 5 in 6
Daljici AB in BC predstavljata par skladnih stranic dolžine a, D pa je četrto oglišče deltoida.
7. korak
Z ravnilom povežemo točki C in D ter poudarimo daljico AD:
Korak 7
Daljici CD in AD predstavljata par skladnih stranic dolžine b.
