Prijava z e-naslovom
Prijava brez gesla
V tem poglavju so predstavljeni koraki za konstruiranje preslikav v geometriji. Med najbolj pogoste preslikave spadata zasuk in zrcaljenje.
Obravnava je osredotočena na preslikavo točke.
Geometrijske elemente in like, ki so v osnovi sestavljeni iz točk, preslikamo tako, da preslikamo njihove robne točke, te pa potem na sliki povežemo v celoto.
Več o obravnavanih preslikavah najdete v poglavju Togi premik v ravnini.
Preden se lotimo risanja, ponovimo definicijo zasuka okoli točke:
Zasuk je predpis, ki poljubni točki T z vrtenjem za kot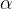 
okoli točke S priredi preslikavo T' :
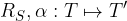
Predpostavimo, da sta točka T, ki jo vrtimo, in točka S, okoli katere vrtimo točko T, že narisani:
1. korak
V šestilo vzamemo razdaljo med točkama T in S.
Šestilo zapičimo v točko S.
S šestilom zarišemo krožnico:
2. korak
Z ravnilom narišemo poltrak, ki ima izhodišče v središču krožnice S in poteka skozi točko T. Poltrak označimo s h:
3. korak
Konstruiramo kot 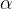z vrhom v točki S tako, da vodoravni krak kota sovpada s poltrakom h.
Točko, v kateri poševni krak kota 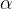seka krožnico, označimo s T':
Točka T' predstavlja zasuk točke T okoli točke S za kot .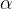
Zrcaljenje čez točko konstruiramo na podlagi poznavanja konstrukcije daljice.
Preden se lotimo risanja, ponovimo definicijo zrcaljenja čez točko:
Zrcaljenje čez točko je predpis, ki poljubni točki T priredi zrcalno sliko T' glede na točko A:
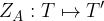
Predpostavimo, da sta točka T, ki jo zrcalimo, in točka A, čez katero zrcalimo točko T, že narisani:
1. korak
Z ravnilom narišemo premico skozi točki T in A ter jo označimo s p:
2. korak
Šestilo zapičimo v točko A.
V šestilo vzamemo razdaljo med točkama T in A:
3. korak
Položaja krakov šestila ne spreminjamo.
S šestilom prenesemo razdaljo med točkama T in A preko točke A (zarišemo polkrog tako, da seka premico p):
Tako nastalo presečišče označimo s točko T':
Točka T' predstavlja zrcalno sliko točke T pri zrcaljenju čez točko A.
Zrcaljenje čez premico konstruiramo na podlagi poznavanja konstrukcije pravokotnice in daljice.
Preden se lotimo risanja, ponovimo definicijo zrcaljenja čez premico:
Zrcaljenje čez premico je predpis, ki poljubni točki T priredi zrcalno sliko T' glede na premico p:
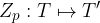
Predpostavimo, da sta točka T, ki jo zrcalimo, in premica p, čez katero zrcalimo točko T, že narisani:
1. korak
Konstruiramo pravokotnico na premico p skozi točko T in jo označimo s q.
Presečišče premic označimo s točko A:
2. korak
Šestilo zapičimo v točko A.
V šestilo vzamemo razdaljo med točkama T in A:
Položaja krakov šestila ne spreminjamo.
S šestilom prenesemo razdaljo med točkama T in A preko premice p (zarišemo polkrog tako, da seka premico q):
Tako nastalo presečišče označimo s točko T':
Točka T' predstavlja zrcalno sliko točke T pri zrcaljenju čez premico p.
