Osebne zbirke


Fant potiska voziček v klanec. Na voziček deluje s silo, ki povzroči, da se voziček giblje. Ugotovi, da je pretežak, zato pokliče na pomoč prijatelja. Sedaj vlečeta z dvojno silo, saj sta sili rok obeh prijateljev vzporedni in delujeta v isto smer.
Otrok brca žogo. S silo noge povzroči, da žoga odleti proti golu. Utež obesimo na elastično vrv. Vrv se raztegne. Avion leti po zraku. Kamen pade na tla. Vsi ti pojavi in še mnogo več so posledica delovanja sile.
Sile pa lahko delujejo tudi tako, da telo stabilno miruje (npr. svinčnik na mizi stabilno miruje). To ne pomeni odsotnosti sil, pač pa, da so si sile v ravnovesju. Njihov skupen vpliv na telo je enak nič. Pravimo tudi, da je njihova vsota ali rezultanta enaka nič in je zato telo v stabilnem stanju - v ravnovesju.
Sila je pojem, ki je opisan v več gradivih:
gradivi Sila in pospešek in Sile pri kroženju opisujeta silo na gibajoče telo;
v Sila trenja in lepenja spoznamo sili, ki se upirata gibanju;
Navor opisuje navor;
v gradivu Gravitacija spoznamo Newtonov zakon gravitacije in Keplerjeve zakone o gibanju nebesnih teles;
A silo bomo spoznavali postopoma. V tem poglavju se bomo osredotočili na osnovne pojme, ki so povezani s silo: ugotovili bomo, da je to vektor in utrdili nekaj matematičnega znanja o vektorjih. Na ta način se bomo obenem naučili s silami tudi računati.
Sila je vektorska fizikalna veličina. Oznaka za silo je F, enota pa N (Newton).
Obstoj sile ugotavljamo v fiziki posredno tako, da opazujemo njen vpliv na telo, na katerega deluje. Na drugo telo lahko sila deluje tako, da:
telesu spremeni hitrost gibanja - glej Sila in pospešek,
telesu spremeni smer gibanja - glej Sile pri kroženju,
telo deformira - glej Vzajemno delovanje sil.
Vpliv sile na drugo telo je lahko:
preko neposrednega stika med silo in telesom.
vpliv na daleč. Vsi poznamo silo teže 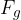 . Ta deluje na daleč in je posledica privlačne sile med telesom in Zemljo (glej poglavje Gravitacija).
. Ta deluje na daleč in je posledica privlačne sile med telesom in Zemljo (glej poglavje Gravitacija).
Ker je sila vektor, ima - tako kot vsak vektor - svoje prijemališče, velikost in smer (glej sliko 1):
prijemališče sile je točka, na katero deluje sila na telo;
velikost sile grafično predstavimo tako, da je dolžina usmerjene daljice sorazmerna velikosti sile;
smer sile grafično označimo s puščico.
V določenih primerih ima lahko sila enak vpliv na telo četudi ima različna prijemališča. Poglejmo si to natančneje na konkretnem primeru:
Ker je vektorska narava sile izjemno pomembna za razumevanje in računanje sil, bomo v nadaljevanju povzeli del matematičnega znanja o vektorjih. Spoznali bomo:
Kaj pomeni vzporedni premik vektorja sile in zakaj ga uporabljamo pri grafičnih prikazih in izračunih vsote.
Kako sile (vektorsko) seštevamo.
Kaj je nasprotna sila in kako jo uporabimo za (vektorsko) odštevanje sil.
Kako razstavimo silo na komponente?
Kaj je ravnovesje sil.
Sila je vektor. Ima svojo:
velikost
smer
prijemališče.
Prijemališče je točka, preko katere deluje sila na drugo telo.
Silo spoznamo posredno in sicer tako, da ugotavljamo njen vpliv na drugo telo. Telesu lahko spremeni hitrost ali smer gibanja ali pa ga deformira. Sila na drugo telo lahko deluje:
v neposrednem stiku s telesom;
na daleč.
Nad silami, podobno kot nad vsemi vektorji lahko izvajamo različne računske oparacije (glej Operacije z vektorji). Omejimo se na naslednje operacije:
vzporedni premik,
seštevanje sil,
odštevanje sil.
Pri seštevanju (ali odštevanju) sil dobimo vektorsko vsoto sil. Pravimo ji tudi rezultanta.
Ko seštevamo sile, jih moramo seštevati vektorsko. Upoštevati je treba smer in velikost sil. Pri tem lahko uporabljamo grafični pristop, znanje geometrije ali vektorski račun. Rezultat, ki ga dobimo, se imenuje vsota ali rezultanta sil.
Pri seštevanju sil si lahko pomagamo z vzporednim premikom sil. To matematično vektorsko pravilo pravi, da se vektor ohrani, če ga vzporedno premaknemo po ravnini ali prostoru.
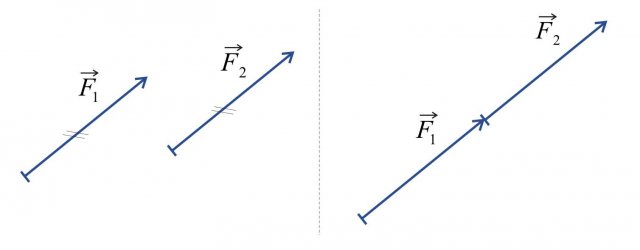
Slika 3: dva vektorja na levi sliki (ali pa le enega izmed niju) lahko vzporedno premaknemo tako, da npr. oba postavimo vzdolž ene osi (kot prikazano na sliki desno).
Če sta vektorja:
enako velika in
imata enako smer
njuno enakost naznačimo z dvema vzporednima črticama (slika 3, levo). V tem primeru velja:
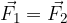
Pravilo s pridom uporabljamo, ko pri seštevanju in odštevanju sile vzporedno premikamo po ravnini.
Pri vzporednih premikih pa se ne ohrani prijemališče vektorja. Zato je to le matematični pripomoček, ki ga uporabimo pri seštevanju sil. Po izvršeni operaciji seštevanja vektor ponovno postavimo v začetno prijemališče.
Dve sili sta nasprotni, če sta enako veliki in nasprotno usmerjeni. V tem primeru se na zunaj izničita. To pomeni, da ne vplivata na okolico, kot smo spoznali v uvodnem poglavju. Njuna vsota ali rezultanta je enaka nič.
Sili na sliki 4 sta enako veliki, a nasprotno usmerjeni. Njuna vsota je zato enaka nič:
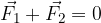
oziroma:
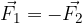
Negativno silo glede na prvotno silo dobimo tako, da vektorju sile ohranimo velikost, le usmerimo ga v nasprotno smer. Posledično, če seštejemo silo in njeno nasprotno silo, je njuna rezultanta enaka 0.
V poglavju Sila in pospešek bomo spoznali, da če na telo delujeta dve nasprotni sili, telo miruje.
Pri seštevanju več sil, med seboj seštevamo posamezne sile, ki jim pravimo komponente. Vsota komponent nam da novo silo, ki ji pravimo rezultanta. Za rezultanto je značilno, da je njen vpliv na telo enak, kot je vpliv vseh komponent na telo skupaj.
Pri iskanju rezultante v praksi vedno narišemo skico, ki ni namenjena samo grafičnemu reševanju nalog, pač pa nam olajša predstavo pri računanju s silami.
Grafično seštevamo sile na dva načina:
s pomočjo paralelogramskega pravila;
s pomočjo mnogokotnika sil.
Vzemimo dve sili z istim prijemališčem, kot kaže slika 5:
Dve sili seštejemo po paralelogramskem pravilu s pomočjo naslednjega postopka:
Sili, ki ju nameravamo sešteti vzporedno premaknemo tako, da imata isto priemališče (modri puščici).
Prvi sili narišemo vzporednico in jo premaknemo na konec druge sile (zelena daljica).
Na enak način tudi drugi sili narišemo vzporednico in jo premaknemo na konec prve sile (zelena daljica).
Modri puščici skupaj z zelenima vzporednicama tvorita paralelogram. Povežemo prijemališče obeh sil z nasprotnim ogliščem in dobim vsoto ali rezultanto (rdeča puščica).
Naj bo danih več sil. Sile lahko seštejemo tako, da:
narišemo prvo silo (ni pomembno katero);
nato postavimo izhodišče druge sile (spet ni pomembno katera je druga sila) v konec prve sile;
vzamemo poljubno tretjo silo in jo vzporedno prenesemo na konec druge sile.
Postopek ponavljamo do zadnje sile.
Povežemo začetek prve in konec zadnje sile in dobimo razultanto. Rezultatna je vsota vektorjev / sil je:
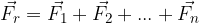
Vektor rezultante lahko z vzporednim premikom ponovno prestavimo.
Sile grafično seštevamo s pomočjo paralelogramskega pravila ali s pomočjo mnogokotnika sil.
Paralelogramsko pravilo
Pri tem pravilu lahko seštevamo samo dva vektorja istočasno. Potegnemo vzporednico k prvemu vektorju in jo postavimo na konec drugega vektorja. Enako naredimo z drugim vektorjem. Dobimo paralelogram. Diagonala paralelograma je rezultanta.
Mnogokotnik sil
Vse sile imajo isto prijemališče npr. v koordinatnem izhodišču. Sile zapovrstjo vzporedno premikamo tako, da je začetek druge sile in koncu prve sile, začetek tretje sile na koncu druge sile itd. Na koncu povežemo začetek prve sile in konec četrte sile in dobimo rezultanto
Sili 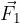 odštejemo silo
odštejemo silo 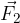 tako, da ji prištejemo nasprotno silo (glej sliko 8):
tako, da ji prištejemo nasprotno silo (glej sliko 8):
Silo 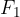 vzporedno premaknemo na mesto, kjer bomo risali konstrukcijo.
vzporedno premaknemo na mesto, kjer bomo risali konstrukcijo.
Sili 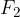 spremnimo predznak - in smer. S tem smo vektorju sile obrnili predznak in dobili vektor
spremnimo predznak - in smer. S tem smo vektorju sile obrnili predznak in dobili vektor 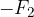 .
.
Na konec vektorja 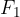 vzporedno prištejemo negativno predznačen (in nasprotno usmerjen) vektor sile
vzporedno prištejemo negativno predznačen (in nasprotno usmerjen) vektor sile 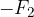 .
.
Povežemo začetek prvega vektorja in konec drugega vektorja. Dobimo rezultanto:
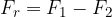
Postopek odštevanja še narišimo:
Vzporedne sile seštevamo na enak način kot pri mnogokotniku. Sil vzporedno premikamo in njihovo izhodišče vedno postavimo v konec predhodnje sile (pri tem pazimo, da negativni sili spremenimo smer). Na koncu povežemo začetek prve sile in konec zadnje sile. Dobimo vsoto ali rezultanto.
Na sliki 9 seštevamo dve pozitivni sili 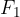 in
in 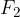 in ji nato prištejemo negativno silo
in ji nato prištejemo negativno silo 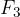 . Povežemo začetek
. Povežemo začetek 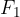 in konec
in konec 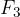 in dobimo rezultanto:
in dobimo rezultanto:
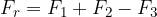
Razstavljanje sile F na komponente je obraten postopek kot paralelogramsko seštevanje sil. Če smo pri paralelogramskem seštevanju (v ravnini) dve sili sešteli v eno samo, pa pri razstavljanju sile eno samo silo (v ravnini) razstavimo na dve komponenti. Predno silo razstavimo na komponente, moramo imeti podane smeri komponent.
Poglejmo si primer razstavljanja sile.
Sile, ki delujejo na izbrano telo, so v ravnovesju takrat, ko je njihova rezultanta enaka nič. Takrat telo miruje ali pa se giba enakomerno in premočrtno (glej poglavje Sila in pospešek). Vedno, ko v naravi opazujemo mirujoče telo, vemo, da so si vse sile ki delujejo na telo v ravnovesju. Njihova rezultanta je enaka nič.
Videli smo že, da imata dve enako veliki, nasprotni sili rezultanto enako nič. Če na telo deluje taka dvojica sil, je telo v ravnovesju.
Opazujmo sedaj ravnovesje z mnogokotnikom sil. Sile so v ravnovesju, če se zaključi mnogokotnik sil tako, da konec zadnje sile natanko sovpade z začetkom prve sile (glej slika 11).
Sile, ki delujejo na izbrano telo, so v ravnovesju, če je njihova rezultanta enaka nič. Takrat telo miruje ali pa se giba enakomerno in premočrtno.
Ta del je namenjen le učencem, ki so osvojili trigonometrične funkcije. Sicer lahko vaje, vezane na to poglavje, rešujemo tudi brez znanja trigonometrije, a le če imamo podane vektorje, ki z abcisno osjo oklepajo "lepe" kote, kot npr. 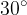 ,
, 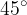 in
in 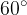 . V tem primeru si pri razstavljanju vektorjev na komponente lahko pomagamo tudi z znanjem geometrijskih likov, npr. kvadrata in enakostraničnega trikotnika.
. V tem primeru si pri razstavljanju vektorjev na komponente lahko pomagamo tudi z znanjem geometrijskih likov, npr. kvadrata in enakostraničnega trikotnika.
Naj bodo v kartezičnem koordinatnem sistemu dani vektorji s prijemališčem v koordinatnem izhodišču. In vsakega od posameznih vektorjev želimo razstaviti na dve komponenti:
komponento, ki deluje v smeri osi x, 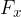 ;
;
komponento, ki deluje v smeri osi y, 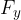 .
.
Zaradi lažjega razumevanja vzemimo primer dveh vektorjev; postopek za izračun rezultante večih vektorjev je podoben.
Vektorje (puščici na sliki 13) lahko seštevamo v kartezijevem koordinatnem sistemu tako, da jih najprej razstavimo na komponente v smeri osi x in y (črtkane črte na sliki 13).
Komponente lahko v splošnem zapišemo s pomočjo funkcij sinus in kosinus:
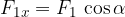
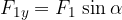
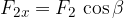
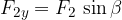
Rezultančni vektor ima x komponento, ki je vsota x komponent posameznik vektorjev in y komponento, ki je vsota y komponent posameznih vektorjev:
Komponente rezultančnega vektorja zapišemo kot vsoto ustreznih komponent osnovnih vektorjev:
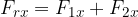
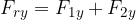
Absolutno vrednost rezultančnega vektorja dobimo po Pitagorovem izreku:
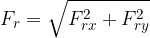
kot rezultačnega vektorja pa s pomočjo funkcije tangens:
