Osebne zbirke

Središčni razteg je poseben primer podobnostne preslikave. Definiramo ga kot:
Središčni razteg je preslikava, ki spremeni velikost množice, ohrani pa njeno obliko.
Oglejmo si središčni razteg na primeru preslikave trikotnika:
S slike je razvidno, da se vse premice, ki povezujejo originale s svojimi slikami, stekajo v točki O. Točko O imenujemo tudi središče raztega. Ta točka je pri raztegu negibna oziroma se preslika sama vase.
Za zgornjo sliko veljajo naslednje enakosti:

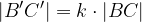
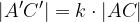
Velja pa tudi:
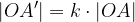
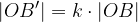
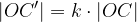
Faktor k, ki se pojavlja v enačbah, je koeficient podobnosti, ki smo ga že spoznali v poglavju o podobnosti. Kadar je koeficient podobnosti enak 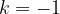 , središčni razteg postane togi premik, točneje preslikava čez točko O.
, središčni razteg postane togi premik, točneje preslikava čez točko O.
Iz gornje slike lahko razberemo lastnosti središčnega raztega:
vsaki točki pri določenemu koeficientu podobnosti pripada natančno ena slika in obratno (bijektivna preslikava v obe smeri)
preslikava ohranja naklon premic, daljic, stranic likov,...
preslikava NE ohranja dolžine daljic
preslikava ohranja velikost kotov
preslikava ohranja orientacijo likov
Dodajmo: če obstaja središčni razteg, ki en geometrijski lik preslika v drugega, za ta dva lika velja, da sta si podobna.