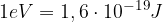Osebne zbirke


Električno nabit delec lahko miruje, se giblje enakomerno ali enakomerno pospešeno. Veljata namreč 1. in 2. Newtonov zakon:
Če je rezultanta vseh sil, ki delujejo na delec nič, delec miruje ali pa se giblje enakomerno in premočrtno.
Če na delec deluje stalna sila, se giblje enakomerno pospešeno.
Naj bo električno nabit delec v električnem polju. Na njega deluje stalna električna sila. Druge sile, npr. gravitacijsko silo, ta trenutek zanemarimo. Zaradi delovanja stalne sile, se bo delec enakomerno pospeševal ali pa se gibal enakomerno pojemajoče.
Če deluje stalna električna sila v smeri gibanja delca, se giblje enamerno pospešeno. Pospešek je pozitiven.
Če deluje električna sila v nasprotno smer gibanja delca, je njegovo gibanje enakomerno pojemajoče. Pospešek je negativen.
Gibajoč električno nabit delec ima tudi svojo maso. Gibajoča masa ima kinetično energijo. Enota za energijo je Joule [J]. V fiziki osnovnih delcev večkrat uporabljamo manjšo enoto - elektronvolt [eV]. Kaj pomeni ta enota bomo spoznali v nadaljevanju.
Postavimo električno nabit delec v električno polje. Na njega prične delovati sila, usmerjena vzdolž silnic električnega polja. Če je naboj pozitiven, deluje sila v smeri silnic električnega polja, če je negativen, pa v nasprotno smer. Velikost električne sile je:
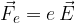
V skladu z 2. Newtonovim zakonom se bo delec pričel gibati enakomerno pospešeno s pospeškom a:
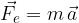
Če izenačimo desni strani obeh enačb:
Na električno nabit delec v električnem polju deluje električna sila. Sila povzroči, da se delec giblje enakomerno pospešeno s pospeškom:
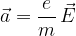
Če poznamo pospešek električno nabitega delca, lahko izračunamo tudi njegovo hitrost po določenem času gibanja in pot, ki jo je preletel. Pri tem uporabimo znanje in enačbe, ki smo se jih naučili v gradivih Enakomerno pospešeno gibanje in Vodoravni met.
Poglejmo si vsa možna gibanja tako, da jih razdelimo na:
gibanje, ki se odvija le na premici (linearno gibanje),
gibanje, ki se odvija na ravnini (ravninsko gibanje).
Možni so naslednji primeri (linearnega) gibanja. Vsa gibanja so enakomerna pospešena gibanja.
Delec v času t = 0 miruje, nakar se prične gibati s pospeškom a.
Njegova hitrost narašča in je v času t:
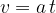
Pot, ki jo je naredil v času t pa je:
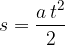
Delec ima v času t = 0 začetno hitrost 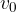 . Zatem mu hitrost narašča s pospeškom a.
. Zatem mu hitrost narašča s pospeškom a.
Njegova začetna hitrost še narašča in je v času t:
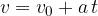
Pot, ki jo je naredil v času t pa je:
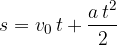
Delec ima v času t = 0 začetno hitrost 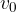 , nakar mu hitrost pada s pojemkom a.
, nakar mu hitrost pada s pojemkom a.
Njegova hitrost v času t je:
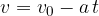
Pot, ki jo je naredil v času t pa je:
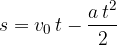
V ravninskem gibanju obravnavajmo primer, ko se delec giblje:
enakomerno vzdolž x osi s hitrostjo 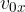
ko začne v času t = 0 delovati na njega električna sila, ki povzroči, da se delec giblje v y smeri s pospeškom a.
Računa se podobno, kot pri vodoravnem metu.
Izračun hitrosti
V času t ostaja x komponenta hitrosti delca enaka, saj je gibanje v to smer enakomerno:
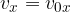
y komponenta hitrosti narašča s pospeškom a:
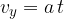
Skupna hitrost je vektorska vsota obeh komponent.
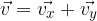
Njegovo absolutno vrednost izračunamo po Pitagorovem izreku, kot pa s pomočjo kotnih funkcij:
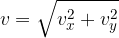
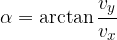
Izračun poti
V času t naredi v x smeri pot:
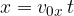
V y smeri pa opravi pot:
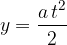
Na električno nabit delec deluje električna sila na poti s. Delo električne sile sile izračunamo z enačbo:
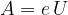
V skladu z izrekom o kinetični energiji, opravljeno delo povzroči spremembo kinetične energije:
Delo električne sile na električno nabit delec je enako spremembi njegove kinetične energije:
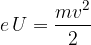
En elektronvolt je energija, ki jo pridobi elektron (z osnovnim nabojem 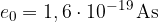 ), ko neovirano preleti potencial 1V:
), ko neovirano preleti potencial 1V: